РАЗВИТИЕ МЕТОДА ЛЯПУНОВА.
Хотя теоремы, приведенные в § 2, полностью решают большинство задач устойчивости, их применение в ряде случаев сложно, поскольку трудно построить функции Ляпунова, удовлетворяющие условиям этих теорем. Имеется ряд других теорем, использующих функции Ляпунова c иными свойствами.
Теорема Барбашина - Красовского. Рассмотрим автономную систему
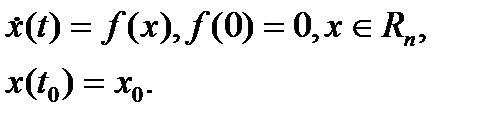 (1)
(1)
Через  обозначим решение системы (1).
обозначим решение системы (1).
Определение 1. Точка 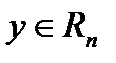 называется
называется  -предельной точкой для точки
-предельной точкой для точки  , если существует последовательность
, если существует последовательность  , такая, что
, такая, что  .
.
Теорема 1. Множество  всех
всех 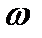 -предельных точек данной точки
-предельных точек данной точки  есть замкнутое множество, состоящее из целых траекторий (рис. 1).
есть замкнутое множество, состоящее из целых траекторий (рис. 1).
Рисунок 1. Структура предельного множества 
□ Замкнутость множества  проверяется следующим образом. Если
проверяется следующим образом. Если 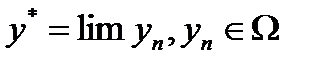 , то
, то 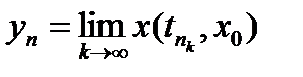 и поэтому
и поэтому 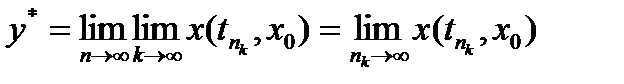 . Далее, если
. Далее, если 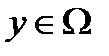 , то обязательно
, то обязательно 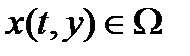 при всех
при всех 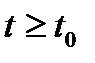 . В самом деле, для любого
. В самом деле, для любого 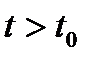 имеем
имеем 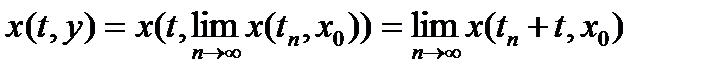 . Поэтому
. Поэтому 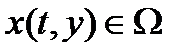 .■
.■
Множество, состоящее из целых траекторий, называют инвариантным множеством. Если 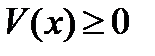 - некоторая функция Ляпунова и
- некоторая функция Ляпунова и 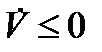 , то все
, то все  -предельные точки для данной точки
-предельные точки для данной точки 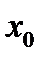 лежат на одной поверхности уровня функции
лежат на одной поверхности уровня функции 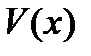 , т. e. для
, т. e. для  имеет место равенство
имеет место равенство  . В самом деле, если
. В самом деле, если 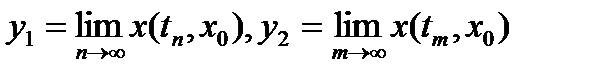 , то в силу непрерывности
, то в силу непрерывности 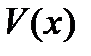 получим
получим
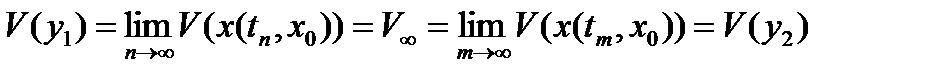 .
.
Теорема 2 (Е. A. Барбашин, Н. П. Красовский). Пусть существует функция Ляпунова 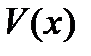 такая, что
такая, что  , причем множество
, причем множество 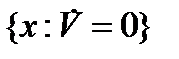 не содержит целых траекторий системы (1), кроме точки
не содержит целых траекторий системы (1), кроме точки 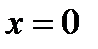 . Тогда тривиальное решение уравнения (1) асимптотически устойчиво.
. Тогда тривиальное решение уравнения (1) асимптотически устойчиво.
□ Решение 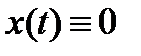 устойчиво, т. e. для заданного
устойчиво, т. e. для заданного 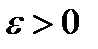 найдется такое
найдется такое 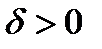 , что
, что 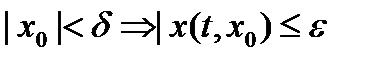 . Пусть
. Пусть 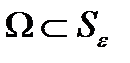 — множество
— множество  - предельных точек для некоторого
- предельных точек для некоторого 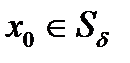 . Покажем, что
. Покажем, что 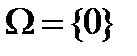 . Предположим, что это не так. Тогда существует
. Предположим, что это не так. Тогда существует 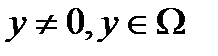 . Поскольку
. Поскольку 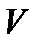 определенно положительна, имеем
определенно положительна, имеем  . Согласно теореме 1, траектория
. Согласно теореме 1, траектория 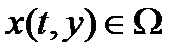 ; поэтому
; поэтому 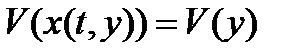 . Значит,
. Значит, 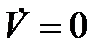 вдоль траектории
вдоль траектории  , т, e.
, т, e. 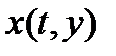 должно принадлежать такому множеству, где
должно принадлежать такому множеству, где 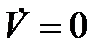 . Но по условию множество
. Но по условию множество 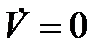 не содержит целых траекторий. Из полученного противоречия вытекает утверждение теоремы.■
не содержит целых траекторий. Из полученного противоречия вытекает утверждение теоремы.■
Если уравнение 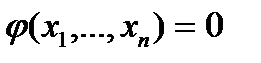 описывает множество
описывает множество 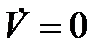 , то условие
, то условие
 (2)
(2)
достаточно для отсутствия целых траекторий во множестве 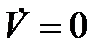 . Заметим, что теорема 2 остается справедливой и для периодических систем.
. Заметим, что теорема 2 остается справедливой и для периодических систем.
Пример 1. Рассмотрим уравнение
 (3)
(3)
Это уравнение описывает колебания материальной точки под действием нелинейной восстанавливающей силы  в среде, сопротивление которой нелинейно зависит от скорости
в среде, сопротивление которой нелинейно зависит от скорости  . Запишем уравнение (3) в виде системы
. Запишем уравнение (3) в виде системы
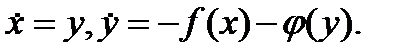 (4)
(4)
Введем функцию Ляпунова
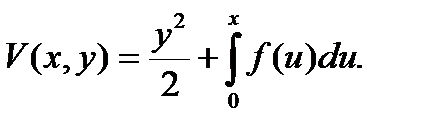 (5)
(5)
Пусть выполнены условия
 (6)
(6)
Тогда функция (5) является определенно положительной, a ее производная равна 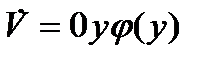 . Множество
. Множество  в данном случае имеет вид
в данном случае имеет вид 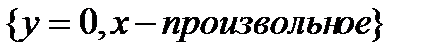 . Но если на некотором решении
. Но если на некотором решении  , то и
, то и 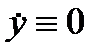 , a значит, и
, a значит, и 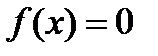 . B силу условий (6) точка
. B силу условий (6) точка  является единственным нулем функции
является единственным нулем функции 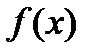 . Следовательно, в множестве
. Следовательно, в множестве 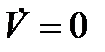 нет целых траекторий, кроме точки
нет целых траекторий, кроме точки 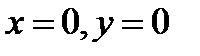 . Согласно теореме 2, тривиальное решение уравнения (3) асимптотически устойчиво, если выполняются неравенства (6). Если, кроме того,
. Согласно теореме 2, тривиальное решение уравнения (3) асимптотически устойчиво, если выполняются неравенства (6). Если, кроме того, 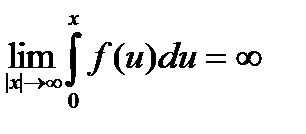 , то в силу теорем 2 и 4 тривиальное решение асимптотически устойчиво в целом.
, то в силу теорем 2 и 4 тривиальное решение асимптотически устойчиво в целом.
2. Критерий Матросова. Теорема Барбашина - Красовского не может быть обобщена на неавтономный случай. В самом деле, для уравнения 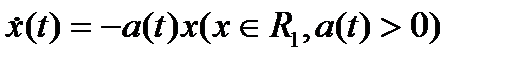 функция
функция 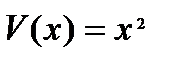 удовлетворяет условиям теоремы 2. В то же время решение
удовлетворяет условиям теоремы 2. В то же время решение 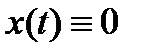 асимптотически устойчиво или нет в зависимости от сходимости или расходимости интеграла
асимптотически устойчиво или нет в зависимости от сходимости или расходимости интеграла  . Для неавтономного уравнения имеет место удобный критерий устойчивости, который получается, если использовать две функции Ляпунова.
. Для неавтономного уравнения имеет место удобный критерий устойчивости, который получается, если использовать две функции Ляпунова.
Теорема 3 (В. M. Матросов). Для равномерной асимптотической устойчивости тривиального решения уравнения необходимо и достаточно, чтобы существовали две функции 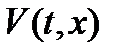 и
и 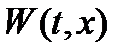 , обладающие следующими свойствами:
, обладающие следующими свойствами:
10) 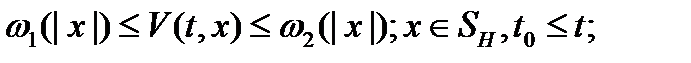
20) 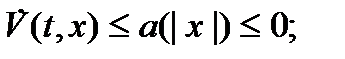
30) 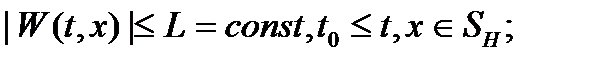
40) 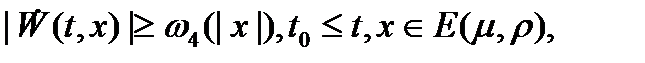
где 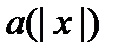 - произвольная непрерывная скалярная функция;
- произвольная непрерывная скалярная функция; 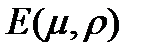 - множество вида
- множество вида 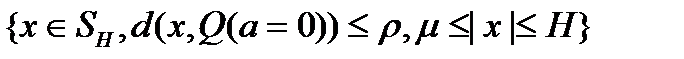 (рис. 2). Здесь
(рис. 2). Здесь 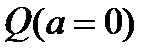 - такое множество из
- такое множество из 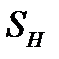 , для которого
, для которого 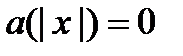 , и
, и 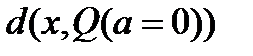 - расстояние от точки
- расстояние от точки 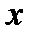 до множества
до множества 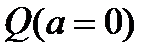 .
.
Пример 2. Маятник с вязким трением, зависящим от времени. Колебания такого маятника (рис. 3) описываются уравнением.
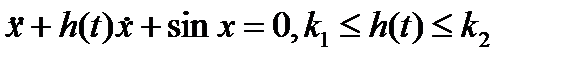 (7)
(7)
или эквивалентной системой
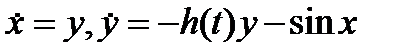 .
.
Рисунок 2. Вид множества 
Рисунок 3. Маятник в среде с вязким трением
Возьмем функцию  в виде
в виде
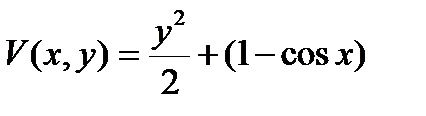 .
.
B области  имеем
имеем
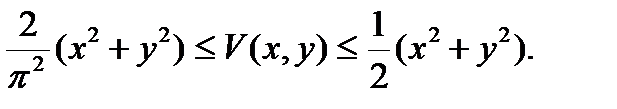
Производная  . Множество
. Множество 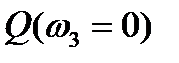 имеет вид
имеет вид 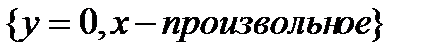 . B качестве второй функции
. B качестве второй функции  возьмем
возьмем 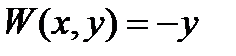 . Она ограничена в любом шаре
. Она ограничена в любом шаре 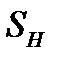 и
и 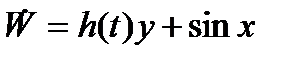 . При
. При 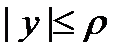 и
и 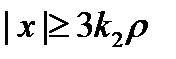 имеем
имеем 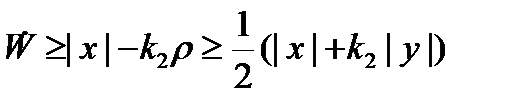 . В силу теоремы 3 тривиальное решение уравнения (7) равномерно асимптотически устойчиво.
. В силу теоремы 3 тривиальное решение уравнения (7) равномерно асимптотически устойчиво.
3. Принцип сравнения. Для решения вопроса об устойчивости сложных или составных систем удобно использовать векторные функции Ляпунова. Сформулируем некоторые результаты.
Рассмотрим уравнение
 . (8)
. (8)
Вектор-функция  называется квазимонотонно возрастающей, если для каждой пары точек
называется квазимонотонно возрастающей, если для каждой пары точек 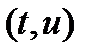 и
и 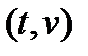 таких, что
таких, что 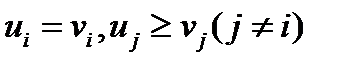 , при всех
, при всех 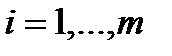 имеет место неравенство
имеет место неравенство 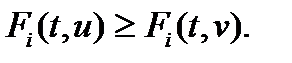 .
.
Теорема 4 (B. М. Матросов). Пусть существует векторная непрерывно дифференцируемая функция 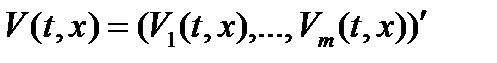 такая, что:
такая, что:
10) 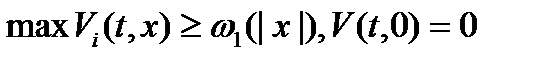 ;
;
20) 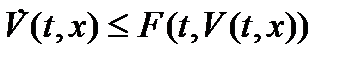 ,
,
Здесь 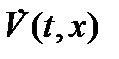 — производная вектор-функции
— производная вектор-функции 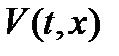 в силу системы (2.1), определяемая формулой
в силу системы (2.1), определяемая формулой
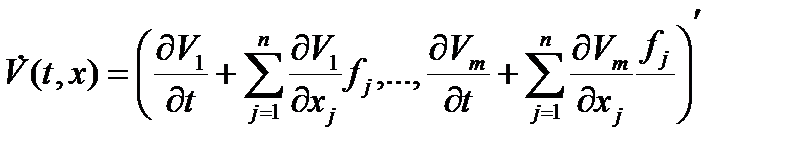
Функция 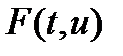 предполагается квазимонотонно возрастающей. Тогда:
предполагается квазимонотонно возрастающей. Тогда:
устойчивость решения 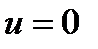 уравнения (8) влечет устойчивость решения
уравнения (8) влечет устойчивость решения 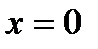 уравнения (2.1);
уравнения (2.1);
равномерная асимптотическая устойчивость решения 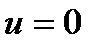 влечет равномерную асимптотическую устойчивость решения
влечет равномерную асимптотическую устойчивость решения 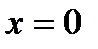 .
.
Пример 3. Рассмотрим систему
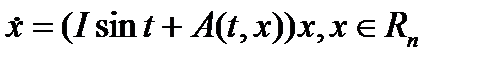 . (9)
. (9)
Здесь 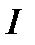 - единичная
- единичная  -матрица, a
-матрица, a 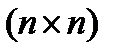 матрица
матрица  c элементами
c элементами 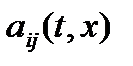 , дифференцируемыми по
, дифференцируемыми по 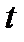 и
и 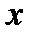 , является кососимметрической, т. е. такой, что
, является кососимметрической, т. е. такой, что 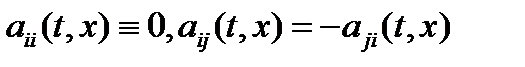 .
.
Возьмем функцию Ляпунова вида
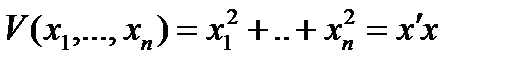 . (10)
. (10)
С учетом кососимметричности матрицы 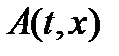 имеем
имеем 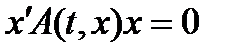 . Поэтому производная функции Ляпунова (10) в силу системы (9) равна
. Поэтому производная функции Ляпунова (10) в силу системы (9) равна
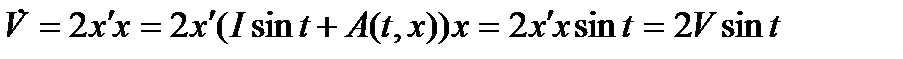 .
.
Производная  функции (10) не знакопостоянна и применить непосредственно теорему Ляпунова 2.1 нельзя. Однако решение
функции (10) не знакопостоянна и применить непосредственно теорему Ляпунова 2.1 нельзя. Однако решение 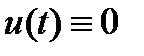 скалярного уравнения
скалярного уравнения 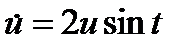 устойчиво, поскольку
устойчиво, поскольку  . По теореме 4 отсюда получаем, что тривиальное решение
. По теореме 4 отсюда получаем, что тривиальное решение 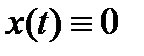 уравнения (9) также устойчиво.
уравнения (9) также устойчиво.
4. Устойчивость, по части переменных. B ряде случаев поведение исследуемой системы таково, что можно ожидать устойчивости только некоторых из фазовых переменных в процессе эволюции этой системы. Так, например, при изучении устойчивости движения велосипедиста нужно только, чтобы отклонения его тела от вертикальной плоскости были малы, a поступательная скорость велосипедиста может меняться в широких пределах. Такой случай удобно изучать c помощью понятия устойчивости по части переменных.
Пусть система описывается уравнениями
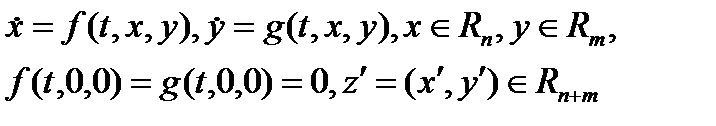 (11)
(11)
Определение 2. Тривиальное решение 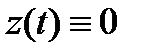
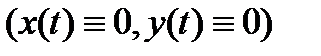 системы (11) называется
системы (11) называется  -устойчивым (устойчивым по отношению к
-устойчивым (устойчивым по отношению к 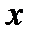 ), если для всякого
), если для всякого 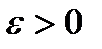 и всякого
и всякого 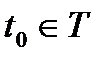 найдется
найдется  такое, что как только
такое, что как только  , выполняется неравенство
, выполняется неравенство 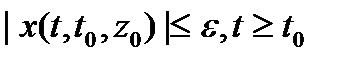 . Решение
. Решение  называется асимптотически
называется асимптотически  -устойчивым, если оно
-устойчивым, если оно  -устойчиво и для некоторого
-устойчиво и для некоторого 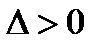 справедливо соотношение
справедливо соотношение 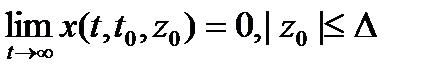 (рис. 4).
(рис. 4).
Рисунок 4. Траектория, устойчивая по переменной 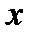 .
.
Теорема 5 (B. В. Румянцев).Пусть существует функция  такая, что:
такая, что:
10) 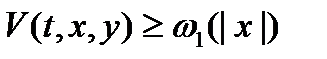 ;
;
20) 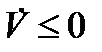 .
.
Тогда решение 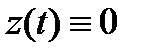 системы (11) является
системы (11) является 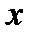 -устойчивым. Если же функция
-устойчивым. Если же функция  такова, что:
такова, что:
30) 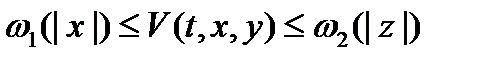 ;
;
40)  ,
,
то решение 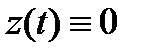 асимптотически
асимптотически 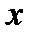 -устойчиво.
-устойчиво.
| <== предыдущая лекция | | | следующая лекция ==> |
| УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ. | | | Второй метод Ляпунова. |
Дата добавления: 2016-03-15; просмотров: 832;
