Час) Разветвление электрической цепи. Правила Кирхгофа.

Непосредственный расчет разветвленных цепей, содержащих несколько замкнутых контуров (контуры могут иметь общие участки, каждый из контуров может иметь несколько источников тока и т.д.) довольно сложен. Эта задача более просто решается с помощью двух правил Кирхгофа (немецкий физик, 1824 – 1887). Любая точка разветвления цепи, в которой сходятся не менее трех проводников с током, называется узлом. При этом ток, входящий в узел считается положительным, а ток, выходящий из узла – отрицательным.

Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:

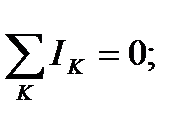(44) или непосредственно по рисунку 17:

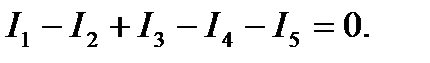
Это правило вытекает из закона сохранения заряда.

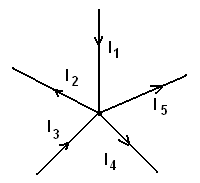
Рис.17

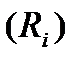Второе правило Кирхгофа: в любом замкнутом контуре (произвольно выбранном в разветвленной электрической цепи) алгебраическая сумма произведений сил токов на сопротивление соответствующих участков этого контура равна алгебраической сумме ЭДС , встречающихся в этом контуре:

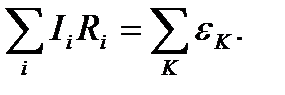(45)

Если направление тока (I) совпадает с направлением обхода, то ток положителен. Если направление обхода от «минуса» к «плюсу» источника, то ЭДС положительна и наоборот.

Пример:

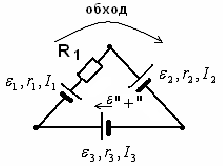
Рис.18

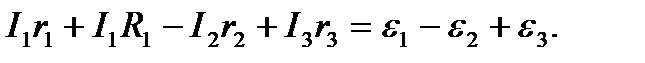
При расчете сложных цепей постоянного тока используют следующий алгоритм:

1. Выбрать произвольное направление токов на всех участках цепи; действительные направления токов определятся после решения задачи; если искомый ток получится положительным, то его направление было выбрано правильным, если отрицательным, то его истинное направление противоположно выбранному.

2. Выбрать произвольно направление обхода контура и строго придерживаться его. Записать произведения токов на сопротивления с учетом знаков и приравнять их сумме ЭДС. Составить уравнения по первому правилу Кирхгофа.

3. По этапам 1 и 2 составить столько уравнений, чтобы их число было равно числу искомых величин. В систему уравнений должны входить все сопротивления и ЭДС цепи.

В качестве примера рассмотрим схему измерительного моста Уинстона (английский физик, 1802 – 1875). Используется для определения неизвестных сопротивлений.

Рис.19

Сопротивления образуют его «плечи». Между точками А и В моста включена батарея с ЭДС ε и сопротивлением r, между точками С и Д включен гальванометр с сопротивлением 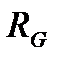. Для узлов А,В, и С, применяя первое правило Кирхгофа, получим: 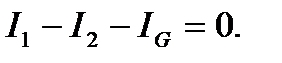(1)

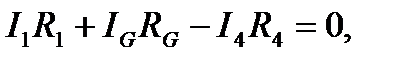
Для контуров АСВА, АСДА и АВДС можно записать: (2)

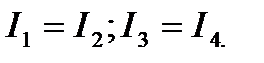Если известны все сопротивления и ЭДС, то, решая полученные шесть уравнений, можно найти неизвестные токи. Изменяя известные сопротивления и можно добиться, чтобы ток через гальванометр был равен нулю , тогда из (1) получим (3). Тогда из (2) получим: и 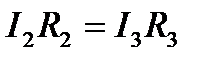(4). Из (3) и (4) получим или (5). Тогда в случае равновесного моста при определении неизвестного (искомого) сопротивления ЭДС батареи, сопротивление батареи и гальванометра роли не играют.

На практике используют реохордный мостик Уинстона, где сопротивления 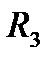и представляют собой одну длинную проволоку с большим удельным сопротивлением. Тогда формула (5) будет . Длины и легко измеряются по шкале, а 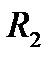всегда известно.

Рис.20

2.3. (1 час) Работа и мощность электрического тока. Закон Джоуля – Ленца. Превращение энергии в электрических цепях.

За время dt через сечение проводника, к которому приложено напряжение U, переносится заряд dq= I·dt, При этом силы электростатического поля (и сторонние силы) совершают работу . (46)

Если из закона Ома ввести в (46) сопротивление R:

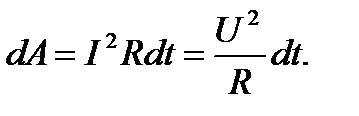(47)

Это формула для работы тока. Из (47) получим мощность тока:

(48)

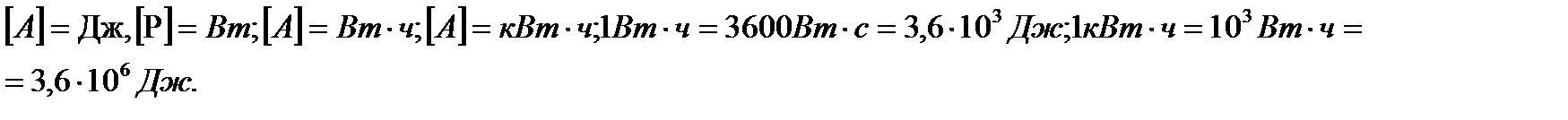
Если работа тока идет на нагревание, то

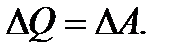(49)

Тогда количество теплоты будет определяться из (47) и (49) по закону Джоуля – Ленца

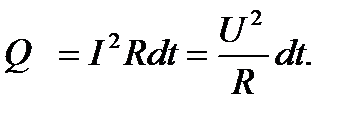(50)

Закон Джоуля – Ленца широко используется в технике: русским инженером Лодыгиным изобретена лампа накаливания (1873), на нагревании проводников электрическим током основано действие электрических (нагревательных) муфельных печей, электрической дуги ( открыта русским инженером В.В.Петровым), контактной электросварки, бытовых электронагревательных приборов и т.д.