час) Контактные явления. Работа выхода электронов. Контактная разность потенциалов. Термоэлектронная эмиссия.
Работа, которую нужно затратить для удаления электрона из металла в вакуум
называется работой выхода. После выхода из металла электрон притягивается индуцированным им положительным зарядом на поверхности металла, а также отталкивается электронами, расположенными дальше вышедшего электрона. Разность потенциалов электрического поля на поверхности металла Δφ, которую должен преодолеть электрон при выходе из металла, называется поверхностной разностью потенциалов (Δφ), которая определяет работу выхода (А) электрона из металла: 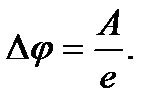
Примеры: для калия А=2,2 эВ, у платины А =6,3 эВ.
В зависимости от способа сообщения электронам энергии различают термоэлектронную, фотоэлектронную, вторичную электронную и автоэлектронную эмиссию.
Термоэлектронная эмиссия – это выход электронов с поверхности металлов при их нагревании. Эмиссия – выпускание, выход.
Фотоэлектронная эмиссия – выход электронов с поверхности металла под действием света, а также коротковолнового электромагнитного излучения (например, рентгеновского).
Вторичная электронная эмиссия – это испускание электронов поверхностью металлов, полупроводников и диэлектриков при бомбардировке их пучком электронов. Используется в фотоэлектронных умножителях.
Автоэлектронная эмиссия – это эмиссия электронов с поверхности металлов под действием сильного внешнего электрического поля. При полях (  ) В/м – возникает такая холодная эмиссия. Эти напряженности сравнимы с напряженностью пробоя воздуха (3 кВ/м) при коронном разряде.
) В/м – возникает такая холодная эмиссия. Эти напряженности сравнимы с напряженностью пробоя воздуха (3 кВ/м) при коронном разряде.
Дополнение:
Теории Максвелла.
В 60-х годах 19-века Д.К.Максвелл, основываясь на идеях Фарадея об электрическом и магнитном полях, обобщил законы, установленные экспериментальным путем, и разработал теорию единого электромагнитного поля.
Математическим выражением теории Максвелла служат четыре уравнения Максвелла, которые принято записывать в двух формах: интегральной и дифференциальной. Уравнения Максвелла в интегральной форме выражают соотношения, справедливые для мысленно проведенных в электромагнитном поле неподвижных замкнутых контуров и поверхностей. Уравнения Максвелла в дифференциальной форме показывают как связаны между собой характеристики электромагнитного поля и плотности электрических зарядов и токов в каждой точке этого поля. Дифференциальные уравнения получают из интегральных с помощью теоремы Гаусса и теоремы Стокса.
6.1. Система уравнений Максвелла в дифференциальной форме:

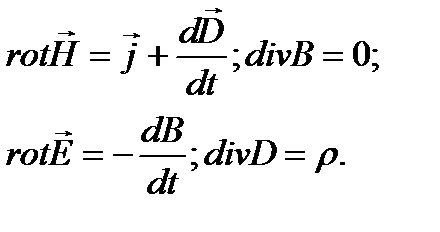
6.2. Уравнения Максвелла в интегральной форме.
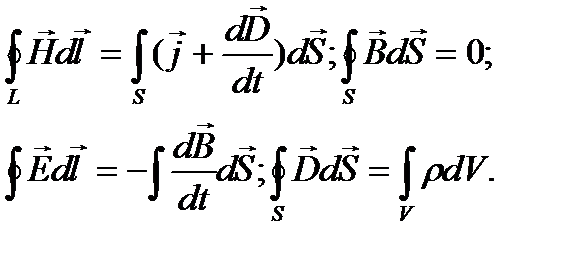

Связь величин:
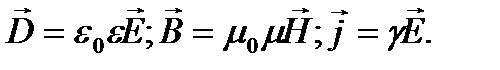
Если поля стационарны, то Е = const и В = const.
Уравнения Максвелла примут вид:
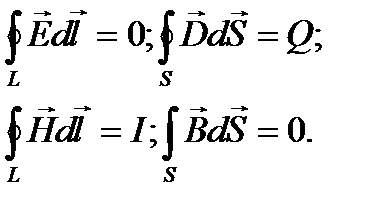
6.3. Уравнение волны:
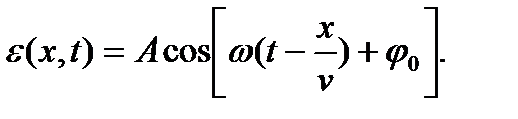
Дата добавления: 2016-03-15; просмотров: 1476;
