Поляризация диэлектриков.
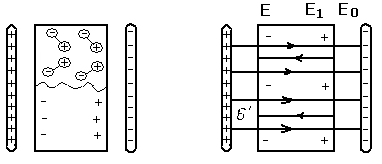
Рис.5
В полярных диэлектриках диполи поворачиваются, а в неполярных и ионных – заряды смещаются.
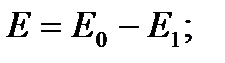
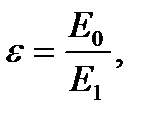 (12) ε – диэлектрическая проницаемость, показывающая во сколько раз внешнее электрическое поле больше поля внутри диэлектрика. (бумага ε = 6, вода ε = 81, полипропилен ε = 2,5).
(12) ε – диэлектрическая проницаемость, показывающая во сколько раз внешнее электрическое поле больше поля внутри диэлектрика. (бумага ε = 6, вода ε = 81, полипропилен ε = 2,5).
Закон Кулона:
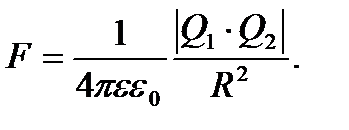 (13)
(13)
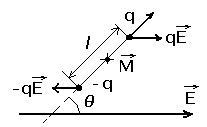
Рис.6
Электрический момент диполя: 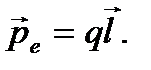 (14)
(14)
Дипольный момент:  (15) или:
(15) или: 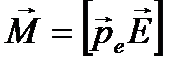 - этот вектор направлен перпендикулярно плоскости векторов
- этот вектор направлен перпендикулярно плоскости векторов 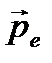 и
и 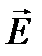 , так что из конца вектора
, так что из конца вектора 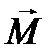 вращение от
вращение от 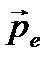 к
к 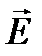 по кратчайшему пути видно происходящим против часовой стрелки.
по кратчайшему пути видно происходящим против часовой стрелки.
Поляризованностью называют дипольный момент единицы объема диэлектрика:
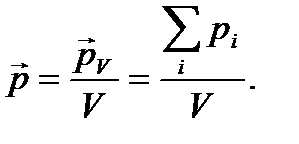 (16)
(16)
Для большинства диэлектриков (за исключением сегнетодиэлектриков) поляризованность линейно зависит от напряженности поля (Е). Если диэлектрик изотропный и  не слишком велико, то
не слишком велико, то
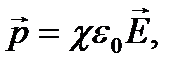 (17) где χ – диэлектрическая восприимчивость вещества:
(17) где χ – диэлектрическая восприимчивость вещества:
χ + 1 = ε, (18) величина безразмерная, причем χ >0. Поляризованность проявляется образованием на поверхности диэлектрика связанных зарядов. Поверхностная плотность ( 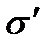 ) связанных зарядов равна поляризованности (р).
) связанных зарядов равна поляризованности (р). 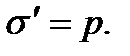 Вектор электрического смещения (поляризации) для электрически изотропной среды:
Вектор электрического смещения (поляризации) для электрически изотропной среды:
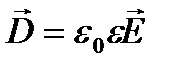 (19) или
(19) или 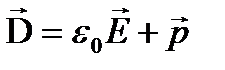 . (20)
. (20)
Единица электрического смещения - 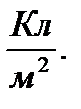 Вектором
Вектором 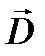 описывается электрическое поле, созданное связанными зарядами.
описывается электрическое поле, созданное связанными зарядами.
Поляризацией диэлектрика называется процесс ориентации диполей или появление под действием внешнего электрического поля ориентированных по полю диполей.
Вектор 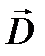 аналогично
аналогично 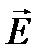 изображается с помощью линий электрического смещения, направление и густота которых определяется точно так же, как и для линий напряженности.
изображается с помощью линий электрического смещения, направление и густота которых определяется точно так же, как и для линий напряженности.
Для произвольной замкнутой поверхности S поток вектора 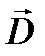 сквозь эту поверхность:
сквозь эту поверхность:
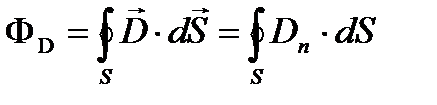 , (21) где
, (21) где 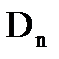 - проекция
- проекция 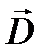 на нормаль
на нормаль 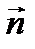 к площадке dS.
к площадке dS.
Теорема Гаусса для электростатического поля в диэлектрике:
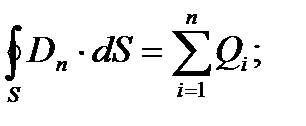 (22) или упрощенно
(22) или упрощенно 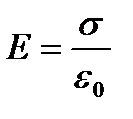 или D=σ.
или D=σ.
Для электростатического поля в вакууме дифференциальное уравнение, называемое уравнением Пуассона:
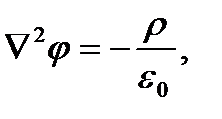 (23) где оператор Лапласа:
(23) где оператор Лапласа:
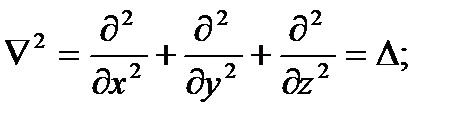 (24) ρ – объемная плотность заряда. В среде
(24) ρ – объемная плотность заряда. В среде 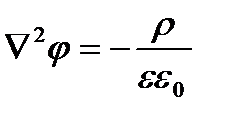 , φ – потенциал поля.
, φ – потенциал поля.
Если в среде нет свободных зарядов, то 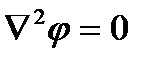 - уравнение Лапласа.
- уравнение Лапласа.
Условия на границе раздела двух сред: пусть ε2 > ε1
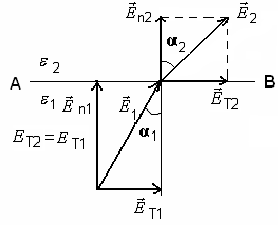
Рис.7
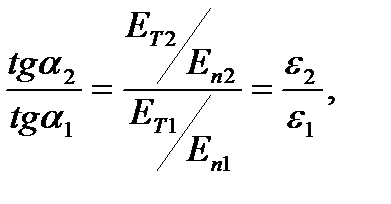 отсюда
отсюда 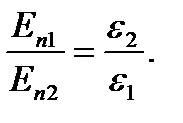 (25)
(25)
На границе двух сред нет свободных зарядов, тогда Еn2 < En1, т.к ε2 > ε1.
Лекция 3.
Дата добавления: 2016-03-15; просмотров: 830;
