Поляризация диэлектриков в электростатическом поле. Свободные, поляризационные заряды в диэлектрике 2 страница
Согласно (5.89) заряд в 1 Кл создаёт через замкнутую воображаемуюповерхность
S площадью ND потоквектора D электрического смещения, равную 1 Кл. Cиловые линии вектора E напряжённости электростатическогополя начинаются и заканчиваются как на qсвободныхтак и на qpсвязанныхзарядах. Cиловые линиивектора D электрического смещенияначинаются и заканчиваются только на qсвободныхзарядах.
Тангенциальные составляющие вектора электрического смещенияи напряжённости электрического поля на границе раздела диэлектриков
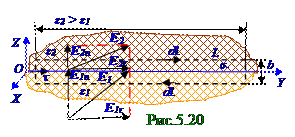
Cиловые линии вектора E напряжённости электрическогополя на рис5.20 находятся в OYZ плоскости. Ось OY является границей между диэлектриками с ε1 и ε2 относительными диэлектрическимипроницаемостями. На границе между диэлектриками с ε1 и ε2 относительными диэлектрическимипроницаемостями находится свободныйq заряд с (5.9) поверхностнойσ плотностью. Прямоугольный L контур a длиной и b шириной находится в OYZ плоскости.
Длина его периметра при b→0 равна 2a. Единичный векторили τ орт направлен по касательнойк границе раздела двух диэлектриковс ε1 и ε2 относительными диэлектрическимипроницаемостями. Проекции векторов E1 и E2 напряжённостей электрического поля на направление τ орта равны соответственно E1τ и E2τ.
|
|
.
электрическогополя (рис.5.20) вдоль L контура равна нулюв любом случае: при отсутствии или наличиина границе между диэлектриками с ε1 и ε2 относительными диэлектрическимипроницаемостямиqсвободногозаряда с σповерхностной плотностью.
Циркуляция вектора E2 напряжённости электрического поля по верхней стороне a длинойзамкнутого L контура с учётом равенства cos(E1 ^dl) = 1, т.к. этот вектор E2 напряжённости электрического поля сонаправлен вектору dl, равен положительной величине E2τa. Циркуляция вектора E1 напряжённости электрического поля по нижней стороне a длиной замкнутого L контура с учётом равенства cos(E2 ^dl) = - 1, т.к. этот вектор E1 напряжённости электрического поля противонаправленвектору dl, равен отрицательной величине "- E1τa". Поэтому (5.41) циркуляция векторов E1 и E2 напряжённостей электрического поля по (рис.6.20) замкнутому L контурус учётом b ширины этогоконтура, стремящейся к нулю, т.е. b→0, имеет следующий вид:

 ∫ Edl= ∫ Edlcos(E ^dl) = E2τa - E1τa = 0 ↔ E1τ = E2τ.(5.90) L L
∫ Edl= ∫ Edlcos(E ^dl) = E2τa - E1τa = 0 ↔ E1τ = E2τ.(5.90) L L
Согласно (5.90) при переходе вектора E напряжённости электрическогополя через границу диэлектриков с различными ε1 и ε2 относительными диэлектрическимипроницаемостями при отсутствии или наличиина границе между этими диэлектриками qсвободногозаряда с σповерхностной плотностью тангенциальная Eτсоставляющая вектора E напряжённости электрическогополя не меняется.
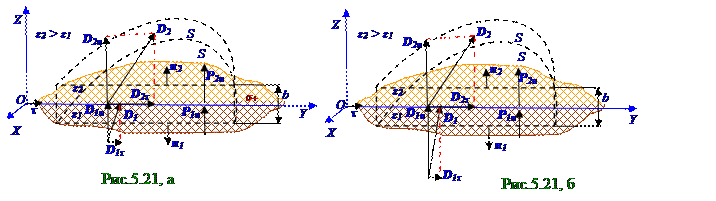
С учётом(5.87) связи вектора D электрического смещенияс векторомE напряжённости электрическогополя D = ε0 εE выражение (5.90) для проекций D1τ и D2τ на направление τ орта вектора D электрического смещенияпринимает следующий вид: D1τ/ε0ε1 = D2τ/ε0ε2 ↔D1τ/D2τ = ε1/ε2.(5.91)Согласно (5.91) при переходе через границу диэлектриков с различными ε1 и ε2 относительными диэлектрическимипроницаемостями при отсутствии или наличиина границе между этими диэлектриками qсвободногозаряда с σповерхностной плотностьюqзарядов тангенциальная Dτсоставляющая вектора D электрического смещенияпретерпевает разрыв. С учётом, например, (рис.5.21, а, б) ε2 > ε1 проекции D1τ и D2τ на направление τ орта вектора D электрического смещения в этих диэлектриках связаны соотношением D1τ < D2τ, что отражено на рис.5.21, а, б меньшей длиной вектора D1τ по сравнению с длиной вектора D2τ.
Нормальные составляющие вектора электрического смещенияи напряжённости электрического поля на границе раздела диэлектриков
Воображаемыйцилиндр с S площадью оснований и b толщиной охватывает диэлектрики с ε1 и ε2 диэлектрическимипроницаемостями при (рис.5.21, а) наличиина границе между диэлектриками qсвободногозаряда с σповерхностной плотностьюи при (рис.5.21, б) отсутствииqмежду диэлектриками qсвободногозаряда с σповерхностной плотностью, т.е. когда σ = 0.
Вектор D электрического смещенияимеет (рис.5.21, а, б) векторы D1 и D2 в диэлектриках с ε1 и ε2 относительными диэлектрическимипроницаемостями.
Поток (5.89) ND вектора D электрического смещения через воображаемый цилиндр
(рис.5.21, а, б) с основанием S площадью, b толщиной при b→0 будет состоять только из нормальных Dn составляющих вектора D электрического смещения.
Поток (рис.5.21, а, б) N2Dвектора D2 электрического смещения через верхнееоснование
S площадьювоображаемогоцилиндра равен положительной величине D2nS, т.к. вектор D2 электрического смещения сонаправлен векторувнешней n2 нормали к этому верхнемуоснованию S площадьювоображаемогоцилиндра.
Поток (рис.5.21, а, б) N1Dвектора D1 электрического смещения через нижнееоснование S площадьювоображаемогоцилиндра равен отрицательной величине "- D1nS ", т.к. вектор D1 электрического смещения противонаправлен векторувнешней n1 нормали к этому нижнемуоснованию S площадьювоображаемогоцилиндра.
В пространстве, охватываемым воображаемымцилиндром с основаниями S площадью и b толщиной, на (рис.5.21, а) границе между диэлектриками с ε1 и ε2 диэлектрическимипроницаемостямиприсутствуют qсвободныезаряды с σповерхностной плотностью, поэтому согласно (5.89) поток NDвектора D электрического смещения через замкнутую поверхность
(рис. 5.21)воображаемогоцилиндра равен всему qсвободному заряду, охватываемомузамкнутойповерхностью этого воображаемогоцилиндра, вследствие чего для этого потока NDвектора D электрического смещения имеет место следующее выражение: ND =D2nS - D1nS = σS ↔ D2n - D1n= σ, (5.92)
где σS - это (рис.5.21, а) весь qсвободныйзаряд, охватываемыйзамкнутойповерхностью воображаемогоцилиндра с основаниями S площадью и b толщиной, т.к. этот qсвободныйзаряд с σповерхностной плотностью сосредоточен только на границе плоской поверхности S площадью между диэлектриками с ε1 и ε2 диэлектрическимипроницаемостями; D1n, D2n - модули векторов D1n, D2n нормальныхсоставляющих вектора D электрического смещениясоответственно в диэлектриках с ε1 и ε2 диэлектрическимипроницаемостями; знак "-" перед D1n поставлен потому, что проекция вектора D1 электрического смещенияв диэлектрике с ε1 диэлектрическойпроницаемостью на внешнюю n1 нормальк нижнему основанию Sплощадьювоображаемогоцилиндра отрицательна.
На рис.5.21, а приведён пример наличия на границе плоской поверхности S площадью между диэлектриками с ε1 и ε2 диэлектрическимипроницаемостями положительного q+свободногозаряда с σ+поверхностной плотностью, т.е. σ+ > 0, поэтому согласно равенству (5.92) D2n > D1n и на рис.5.21, а длина вектора D2n больше длины вектора D1n.
Согласно(5.87) E1n, E2n модули векторов E1n, E2n нормальныхсоставляющих вектора
E напряжённости электрическогополя связаны с модулями D1n, D2n векторов D1n, D2n нормальныхсоставляющих вектора D электрического смещениясоответственно в диэлектриках с ε1 и ε2 диэлектрическимипроницаемостями при (рис. 05.0.21, а) наличиина границе между этими диэлектриками qсвободногозаряда с σповерхностной плотностью с учётом (5.92) следующими выражениями: D1n = ε0ε1E1n ; D2n = ε0ε2E2n ↔ D2n - D1n= σ ↔ ε0ε2E2n - ε0ε1E1n = σ ↔
↔ E2n = (ε1E1n/ε2) + (σ/ε0ε2), (5.93)
где σ - поверхностная плотность свободногозаряда на границе между диэлектриками, которая может σ+ положительной или σ- отрицательной.
Согласно (5.91) при переходевектора E напряжённости электрическогополя через границу диэлектриков с различными ε1 и ε2 диэлектрическимипроницаемостями и при (рис. 05.0.20) наличиина границе между этими диэлектриками qсвободногозаряда с σповерхностной плотностьюE1n, E2n модули векторов E1n, E2n нормальныхсоставляющих вектора E напряжённости электрическогополя претерпевают разрыв.
Величина (рис.5.20) изменения E2n модуля вектора E2n нормальнойсоставляющей в диэлектрике с ε2 диэлектрическойпроницаемостью по сравнению с E1n модулем вектора E1n нормальнойсоставляющей в диэлектрике с ε1 диэлектрическойпроницаемостью вектора E напряжённости электрическогополясогласно (5.93) зависит от отношения ε1/ε2, а также зависит от знака и величины qсвободногозаряда с σповерхностной плотностьюна границе между этими диэлектриками. Например, согласно (5.91) при ε2 > ε1 и отрицательном q-свободномзаряде с σ-поверхностной плотностью на границе между диэлектриками, т.е. σ- < 0, нормальные E1n, E2n составляющие вектора E напряжённости электростатическогополя в этих диэлектриках имеют модули, связанные согласно (5.93) следующим соотношением: E1n > E2n. Это отражено на рис. 05.0.20 при наличии отрицательного q-свободногозаряда с σ-поверхностной плотностью на границе между диэлектрикамибόльшей длиной вектора E1n по сравнению с длиной E2n вектора.
Согласно (5.92) при переходевектора D электрического смещения через границу диэлектриков с различными ε1 и ε2 диэлектрическимипроницаемостями и при
(рис. 05.0.21, б) отсутствии на этой границе q свободныхзарядов, т.е. при равенстве нулю в (5.90) поверхностнойσ плотностиq свободныхзарядов σ = 0,нормальная Dn составляющая вектора D электрического смещения не меняется, что отражено на рис.5.21, б одинаковой длиной
D1n и D2n векторов.
С учётом(5.87) связи вектора D электрического смещенияс вектором E напряжённости электростатическогополя D = ε0 εE имеет место следующее выражение для модулей E1n, E2n нормальных E1n, E2n составляющих вектора E напряжённости электростатическогополя при отсутствии на границе между диэлектриками с ε1 и ε2 диэлектрическимипроницаемостями q свободныхзарядов, т.е. (рис.5.21, б) при равенстве нулю в (5.92) поверхностнойσ плотностиq свободныхзарядов σ = 0: D1n= D2n ↔ E1nε0ε1 = E2nε0ε2 ↔ E1n/E2n = ε2/ε1. (5.94)
Согласно (5.94) при переходе через границу диэлектриков с различными ε1 и ε2 диэлектрическимипроницаемостями при отсутствии на этой границе q свободныхзарядовнормальная Enсоставляющая вектора E напряжённости электростатическогополя претерпевает разрыв, поэтому (рис.5.20), например, при ε2 > ε1 нормальные E1n, E2n составляющие вектора E напряжённости электростатическогополя в этих диэлектриках имеют модули, связанные следующим соотношением: E1n > E2n. Это отражено на рис.5.20 бόльшей длиной вектора E1n по сравнению с длиной вектора E2n.
Нормальные составляющие вектора поляризованности на границе раздела диэлектриков
Вектор P поляризованности диэлектрика имеет векторы P1 и P2 в диэлектриках с ε1 и ε2 относительными диэлектрическимипроницаемостями, коллинеарныхсогласно (5.86) векторам D1 и D2 электрического смещения в этих диэлектриках.
Поток (5.81) Фpвектора P поляризованностидиэлектрика через воображаемый цилиндр
(рис.5.21, а, б) с основанием S площадью, b толщиной при b→0 будет состоять только из нормальных Pn составляющих этого вектора P поляризованностидиэлектрика.
Поток (рис.5.21, а, б) Ф2Pвектора P2 поляризованности диэлектрика через верхнееоснование
S площадьювоображаемогоцилиндра равен положительной величине P2nS, т.к. вектор P2 поляризованности диэлектрикасонаправлен векторувнешней n2 нормали к этому верхнемуоснованию S площадьювоображаемогоцилиндра.
Поток (рис.5.21, а, б) Ф1Pвектора P1 поляризованности диэлектрика через нижнееоснование S площадьювоображаемогоцилиндра равен отрицательной величине "- P1nS ", т.к. вектор
P1 поляризованности диэлектрикапротивонаправлен векторувнешней n1 нормали к этому нижнемуоснованию S площадьювоображаемогоцилиндра.
Согласно (5.81)поток Фpвектора P поляризованности диэлектрикачерез воображаемый цилиндр (рис.5.21, а, б) с основанием S площадью, b толщиной при b→0 будет иметь следующий вид: Фp = ∫PdS= Ф2P + Ф1P = P2nS - P1nS = - qp, (5.95) (S)
где qp- связанныйзарядов в V объёме диэлектрика, ограниченном воображаемымцилиндром с S площадями оснований и (рис.5.21, а, б) находящимся на границе диэлектриков с различными ε1 и ε2 диэлектрическимипроницаемостями.
Граница диэлектриков с различными ε1 и ε2 относительными диэлектрическимипроницаемостями имеет S площадь и на ней находятся поляризационныезаряды с σp поверхностнойплотностью, которые охватывает (рис.5.21, а, б)воображаемыйцилиндр. Поэтому этот воображаемый цилиндр с основанием S площадью, b толщиной при b→0 охватывает qpполяризационныйзаряд, имеющее следующее значение: qp = σpS. (5.96)
Подставляем (5.96) в (5.95) и получаем следующее выражение, связывающее разность проекций P2n, P1n на внешние n2 и n1 нормали вектора P поляризованностив диэлектриках с соответственно ε2 и ε1 диэлектрическимипроницаемостями с σpповерхностнойплотностью поляризационныхзарядов на границе этих диэлектриков:P2nS - P1nS = - σpS ↔ P2n - P1n = - σp, (5.97) где σp - поверхностная плотность поляризационногозаряда на границе между диэлектриками, которая может σp+ положительной или σp- отрицательной.
Выражение (5.97) справедливо (рис. 05.0.21, а) при наличиина границе между диэлектриками qсвободногозаряда с σповерхностной плотностьюили при (рис. 05.0.21, б) отсутствииqмежду этими диэлектриками qсвободногозаряда с σповерхностной плотностью.
Согласно (5.97), если модуль P2n вектора P2n нормальнойсоставляющей поляризованностив диэлектрике с ε2 относительной диэлектрическойпроницаемостью меньше модуля P1n вектора P1n нормальнойсоставляющей поляризованностив диэлектрике с ε1 относительной диэлектрическойпроницаемостью, то на границе этих диэлектриков возникает положительныйполяризационныйзаряд с σp+поверхностной плотностью.
Согласно (5.97), если модуль P2n вектора P2n нормальнойсоставляющей поляризованностив диэлектрике с ε2 диэлектрическойпроницаемостью больше модуля P1n вектора P1n нормальнойсоставляющей поляризованностив диэлектрике с ε1 диэлектрическойпроницаемостью, то на границе этих диэлектриков возникает отрицательный поляризационныйзаряд с σp-поверхностной плотностью. Этот случай отражен на рис.5.21, а, б на границе диэлектриков бόльшей длиной вектора P2n нормальнойсоставляющей поляризованностив диэлектрике с ε2 диэлектрическойпроницаемостью на границе диэлектриков по сравнению с длиной вектора P1n нормальнойсоставляющей поляризованностив диэлектрике с ε1 диэлектрическойпроницаемостью.
Лекция 4 Электрическое поле заряженных проводников. Энергия электростатического поля
Электростатическое поле вблизи поверхности проводника, окружённого диэлектриком. Заряд проводника и поляризационный заряд на поверхности диэлектрика, окружающего проводник. Силы, действующие на поверхность заряженного проводника в вакууме. Электроемкость уединённой проводящей сферической поверхности. Емкость плоского конденсатора. Емкость коаксиального конденсатора. Емкость сферического конденсатора. Энергия взаимодействия системы точечных зарядов в диэлектрике. Собственная энергия заряженных проводников в диэлектрике. Полная энергия заряженных проводников в диэлектрике. Электрическая энергия плоского конденсатора. Энергия электростатического поля в диэлектрике. Работа электростатического поля при поляризации диэлектрика. Электростатические генераторы электрической энергии.
Электростатическое поле вблизи поверхности проводника, окружённого диэлектриком В металлических проводниках имеются носителитока - электроны проводимостиили свободные электроны, которые могут под действием электрического поля перемещаться по всему проводнику. В отсутствие внешнего электроcтатического поля электроны проводимостии положительныеионы металлов взаимно компенсируются. Если металлический проводник внесён во внешнее электроcтатическое поле, то под действием этого поля электроны проводимости, которые превращаются в индуцированныеили наведённыезаряды,перераспределяются в проводнике так, что в любой точке внутри проводникаэлектрическое поле электронов проводимостии положительныхионов компенсирует внешнее электроcтатическое поле. ВекторE напряжённости электростатическогополя у поверхностипроводника направлен по нормалик поверхности этого проводника, т.е. Eτ касательнаяили тангенциальнаясоставляющая вектора E напряжённости электростатическогополя у поверхностипроводника равна нулю. Наличие Eτ касательнойсоставляющей вектора E напряжённости электростатическогополя у поверхностипроводника вызвала бы перемещение носителей тока по этой поверхности проводника, что противоречит условию равновесия зарядов в проводнике, находящемся во внешнем электроcтатическом поле.
Проводники, находящиеся во внешнем электроcтатическом поле,имеютследующиеособенности:
а) всюду внутри проводника векторE напряжённости электростатическогополя равен нулю, а у его поверхности он имеет только En нормальнуюсоставляющую; Eτ касательнаяили тангенциальнаясоставляющая вектора E напряжённости электростатическогополя у поверхностипроводника равна нулю;
б) весь объём этого проводника эквипотенциален, т.к. (5.56) проекция El вектора
E напряжённости электростатическогополя на произвольное направление dl элементарноговектораперемещения внутри проводника равна нулю, вследствие равенстванулю по пункту а)вектора
E напряжённости электростатическогополя внутри этого проводника и это (5.56) выражение принимает следующий вид: El = - dφ/dl = 0 ↔ φ = const, (5.98) где φ - потенциал в любой точке проводника постоянен, т.е. весь объём этого проводника эквипотенциален;
в) поверхность проводника тоже эквипотенциальна, т.к. (5.56) проекция Eτ вектора
E напряжённости электростатическогополя у поверхностипроводника на направление τ вектора, касательного в любой точке поверхностиэтогопроводника, всегда равна нулюи это (5.56) выражение принимает следующий вид: Eτ = - dφ/dτ = 0 ↔ φτ = const, (5.99) где φτ - потенциал в любой точке поверхности проводника постоянен, т.е. вся поверхность этого проводника эквипотенциальна; г) нескомпенсированные положительные(рис.5.22, а) заряды с σ+ поверхностной плотностью или (рис.5.22, б) отрицательной σ - поверхностной плотностью располагаются в проводнике только на его поверхностии по а) пункту всюду внутри проводника вектор E напряжённости электростатическогополя равен нулю.
Дата добавления: 2016-02-14; просмотров: 853;
