Одиночный сигнал можно найти по его спектру обратным преобразованием Фурье.

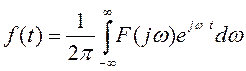
Свойства преобразования Фурье

1. Теорема линейности Если 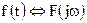, то .

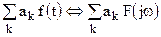2. Теорема о дифференцировании сигнала по времени. Если 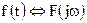, то .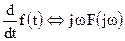

3. Теорема об интегрировании сигнала по времени. Если 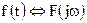, то .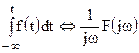

4. Теорема запаздывания ( смещение во времени) Если 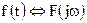, то .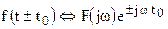

5. Теорема сжатия по времени. Если 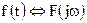, то .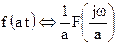

6. Теорема свертки

Если 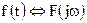, то .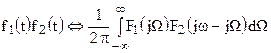

Если 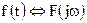, то .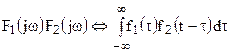

7. Теорема смещения по частоте. Если 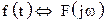, то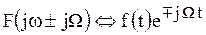

Найдем комплексную спектральную плотность одиночного прямоугольного импульса при симметричном расположении.

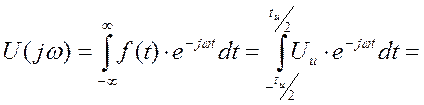
U_u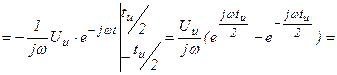

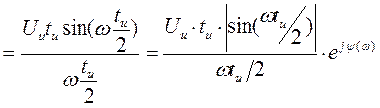
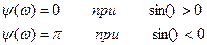
Получается непрерывная функция частоты вида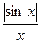

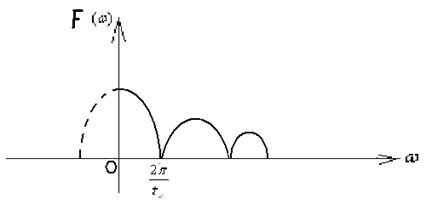
Вывод: Спектр одиночного сигнала похож на спектр последовательности таких же сигналов, точнее соответствует огибающей спектра дискретного сигнала, но размерности у них разные.

Математически спектральная плотность симметричная функция

Рассмотрим несимметричное расположение сигнала.

Найдем его спектр. Это можно сделать напрямую с помощью интеграла Фурье, а можно по теореме запаздывания.

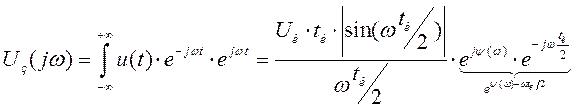
Общий угол Ψ(ω)-ωt_u/2

Спектральная плотность амплитуд не изменяется,