Графическое временное и частотное изображения

Спектра периодического сигнала

временное изображение

частотное изображение АЧС

Аналогично ФЧС, только учитывая, что фазы могут быть и отрицательными.

Такой спектр называется дискретным или линейчатым, он характерен для периодического сигнала.

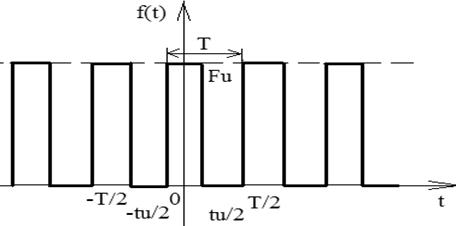
Спектр последовательности прямоугольных импульсов

Рассмотрим симметричное расположение импульсов

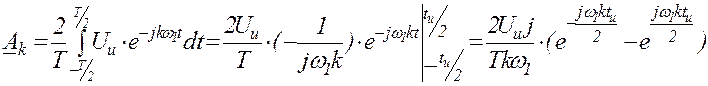
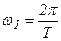
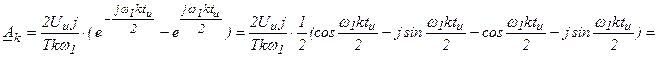
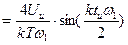
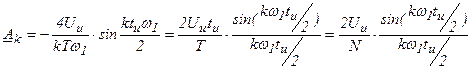, где 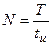- скважность.

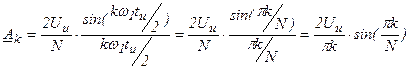
Найдем нулевые точки синуса:

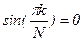
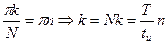
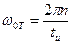Первая нулевая точка – самая важная для спектра последовательности прямоугольных импульсов.

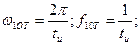
АЧС последовательности прямоугольных импульсов:

ω₁ ω₂ 2π/t_u 4π/t_u

Основную долю энергии несут гармоники, расположенные от 0 до первой нулевой точки (около 90% энергии). Эту область частот, где сосредоточено 90% энергии сигнала, называют шириной спектра (частотного) сигнала.

Для прямоугольного импульса ширина спектра - .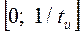

Любая цифровая передача сигнала требует большего спектра, чем простая аналоговая.

ФЧС последовательности прямоугольных импульсов:

если sun(x)>0, то Ψ_k=0

Если длительность уменьшается, то основная частота не изменится, нулевые точки переместятся вправо. До первой нулевой точки, где сосредоточена основная энергия, попадает больше составляющих. Технически отмечают, что спектр расширяется.