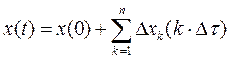Пример нахождения временных характеристик

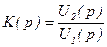
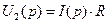
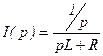
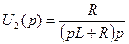
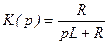
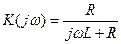
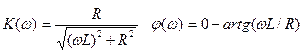
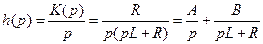
Определив коэффициенты A и B, получаем:

Тогда: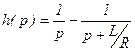

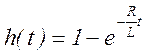
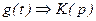
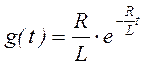
ω=2πf

Расчет откликов в электрической цепи на кусочно-непрерывное воздействие.

(Интеграллы Дюамеля и наложения)

При передаче информации сигналы могут быть сложными функциями, состоящими из отдельных скачкообразных воздействий.

В каждом интервале функция меняется по одному закону.

Разобьем функцию воздействия на элементарные ступеньки

Δτ→0 Δx=x^/ Δτ

Y(t) определяется с помощью переходной характеристики

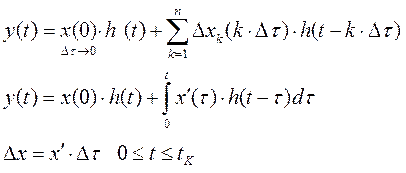Это и есть интеграл Дюамеля

Интеграл наложения основан на разбиении функции воздействия на элементарные импульсы

Реакцию на импульсное воздействие можно найти с помощью импульсной характеристики с учетом площади импульса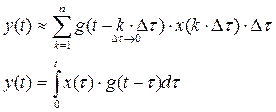

Определение отклика на прямоугольный импульс.

Классический метод

Можно рассчитывать отдельно на включение импульса и на выключение, если за время импульса переходный процесс закончится.

Операторный метод

Находим X(p)=(по Лапласу)

Возьмем для примера цепь:

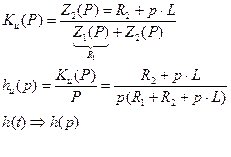
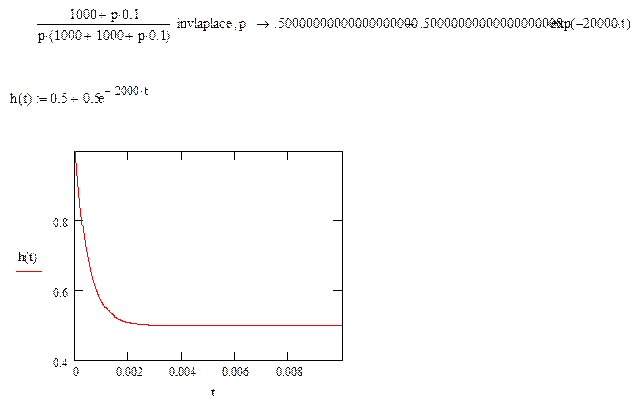
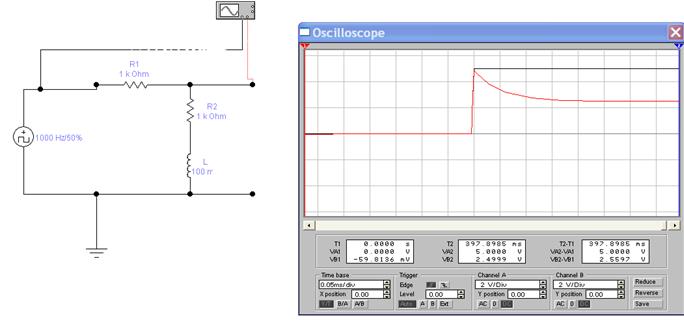
Дифференцирующие и интегрирующие цепи

Общие понятия

При обработке электрических сигналов может возникнуть задача дифференцирования или интегрирования сигнала, т.е. чтобы реакция на выходе цепи была пропорциональна производной или интегралу входного сигнала.

Дифференцирующими и интегрирующими называют цепи, которые имеют на выходе напряжение, пропорциональное производной или интегралу от входного напряжения.

Дифференцирующие цепи