Хевисайдом была разработана теорема разложения сложной функции на простые с последующим определением оригинала, т.е. тока или напряжения, как функции времени.

Т.е. 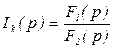, где F₁(p) – полином числителя, F₂(p) – полином знаменателя.

Такую функцию можно разложить на элементарные дроби следующим образом:

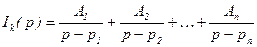. Здесь р_К - корни знаменателя F₂(p).

Тогда оригинал легко ищется в виде суммы экспонент: 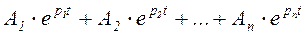. Причем коэффициенты 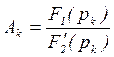. Разложение возможно, если старшая степень числителя меньше степени знаменателя.

Если один из корней равен 0, то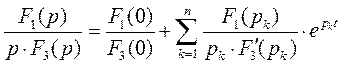

Рассмотрим пример: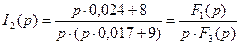

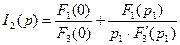
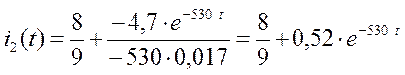
Корни могут быть комплексно-сопряженными. В этом случае пользуются общей формулой, причем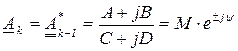

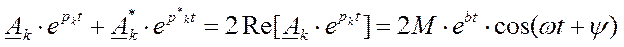, если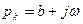

Для цепи с R_i и параллельными LC получиться при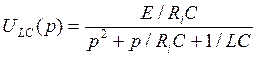

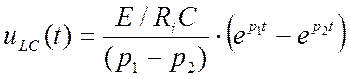
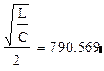R_КР

R=500 Ом R=3000 Ом

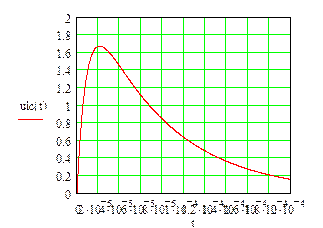
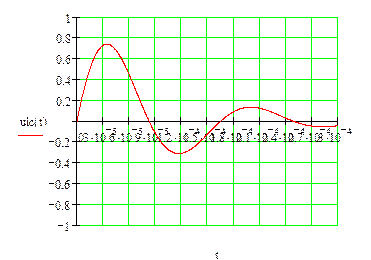
Существует еще четвертый способ нахождения оригинала применением программных средств (Например: MathCad).

Операторные передаточные функции

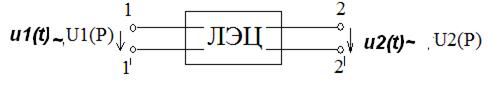
Операторная передаточная функция - это отношение операторного изображения реакции или отклика электрической цепи к операторному изображению воздействия на электрическую цепь. Приминается в основном для линейных цепей при нулевых независимых начальных условиях. Техническое название - операторные коэффициенты передачи. В зависимости от вида воздействия и типа реакции различают четыре варианта коэффициентов передач:

· по напряжению U

· по току I

· по сопротивлению Z

· по проводимости. Y

К_U(p) = Т_U(p) = Н_U(p) = U_{ВЫХ (2)}(p)/U_ВХ(1)(p) К_Z(p) = U₂(p)/I₁(p) К_Y(p) = I₂(p)/U₁(p)

В линейных цепях передаточные функции не зависят от воздействия, а определяются только самой электрической цепью. (Бывают передаточные функции не электрического вида).