Многофакторный дисперсионный анализ

Многофакторный дисперсионный анализ (МДА) позволяет оценивать влияние на наблюдаемую переменную уже не одного, а произвольного числа факторов. Точнее, МДА позволяет выбрать из группы факторов, участвующих в эксперименте, те, которые действительно влияют на его результат.
Методику проведения многофакторного дисперсионного анализа рассмотрим применительно к частичному факторному эксперименту, проводимому в соответствии с латинским планом.

Пусть в эксперименте рассматриваются один первичный фактор и два вторичных, каждый из которых имеет n уровней (то есть объем испытаний равен N=n2). Обозначим через yijk результат эксперимента при условии, что фактор а находился на уровне i, фактор b — на уровне j, фактор с — на уровне k. Множество значений, которые может принимать упорядоченная тройка (i, j, k), обозначим через L. В этом случае уравнение дисперсионного анализа выглядит следующим образом:

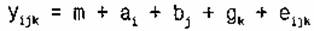
Здесь m — генеральное среднее случайной величины у; аi, bj, gk - неизвестные параметры («эффекты» соответствующих факторов).
Решение задачи дисперсионного анализа заключается в проверке гипотез о независимости результатов измерений от факторов а, b, c:

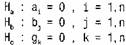
Для этого по методу наименьших квадратов (МНК) находят оценки параметров m, ai, bj, gk, минимизируя по указанным переменным (поочередно) функцию

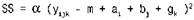
Затем по каждому фактору вычисляется F-статистика. Величина Fесть мера потерь при принятии гипотезы Н0. Чем больше F, тем хуже модель, отвергающая влияние соответствующего фактора. Таким образом, если вычисленное значение F больше FKP, найденного по таблице для некоторого уровня значимости (и n-1, n2-3n+2 степеней свободы), то гипотеза отвергается. Дисперсионный анализ может использоваться для оценки влияния факторов, имеющих как количественный, так и качественный характер, поскольку в уравнении дисперсионного анализа фигурируют не сами факторы, а только их «эффекты».

В том случае, если все факторы носят количественный характер, взаимосвязь между ними и наблюдаемой переменной может быть описана с помощью уравнения регрессии.