Однофакторный дисперсионный анализ

Суть однофакторного дисперсионного анализа сводится к определению влияния на результат моделирования одного выбранного фактора.
Пусть, например, исследователя интересует средняя интенсивность отказов компьютера, и в созданной им модели учтены следующие факторы: интенсивность поступления заданий пользователей, интенсивность обращений в оперативную память, временные характеристики решаемых задач и интенсивность обращений к жесткому диску. Если предварительные данные говорят о том, что основной причиной отказов является ненадежная работа жесткого диска, то в качестве анализируемого фактора целесообразно выбрать интенсивность обращений к нему. Задача анализа в данном случае состоит в том, чтобы оценить влияние указанного фактора на среднее число отказов.

формально постановка задачи однофакторного дисперсионного анализа состоит в следующем. Пусть интересующий нас фактор х имеет l уровней. Для каждого из них получена выборка значений наблюдаемой переменной 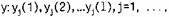n, где n — объем выборки (число наблюдений).
Необходимо проверить гипотезу Н0 о равенстве средних значений выборок (то есть о независимости значений у от значений исследуемого фактора х). Уравнение однофакторного дисперсионного анализа имеет вид:

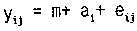
Здесь уij — j -е значение у в i-й серии опытов; m — генеральное среднее случайной величины у (то есть среднее значение наблюдаемой переменной, обусловленное ее «сущностью»); ai — неизвестный параметр, отражающий влияние фактора х («эффект» i-го значения фактора х); eij — ошибка измерения у.

Для проверки гипотезы Н0 используют F-критерий и переходят от проверки значимости различий средних к проверке значимости различий двух дисперсий:

· генеральной (обусловленной погрешностями измерений) — D0;

· факторной (обусловленной изменением фактора х) — DX:

Значение F-критерия вычисляется как отношение DX/D0 или D0/DX (в числителе должна стоять большая из дисперсий); затем по таблице F-распределений находят его критическое значение FKP для заданного уровня значимости и числа степеней свободы m1=n-l, m2=l-1.

Если F>FKР, то гипотезу Н0 отвергают, то есть различия являются значимыми (фактор х влияет на значения у).