ПРИНЯТИЕ СЕТЕВЫХ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ ИСХОДНОЙ ИНФОРМАЦИИ
Можно предположить, что ситуация, возникающая допускает достаточно четкую для количественного анализа формулировку задачи. Это означает, что имеется возможность:
- четко определить смысл принимаемого решения и состав оптимизируемых параметров сети (вектор хpr), где конкретные значения вектора хpr называются «вариантами решения»;
- выявить состав исходных данных, которые имеют неоднозначный характер и создают неопределенность ситуации (вектор ypr), отдельные значение вектора ypr называются «сочетанием информации»;
- построить математическую модель - систему уравнений, отражающую реальные взаимосвязи между параметрами xpr и ypr, а также имеющиеся ограничения;
- записать оценочную функцию З(xpr,ypr), которая количественно характеризует эффект, достигаемый при фиксированных варианте решения xpr и сочетании исходных данных ypr (под оценочной функцией понимается значение критериев оптимизации).
Следует отметить, что функция З(xpr,ypr) не является целевой в обычном смысле (как для детерминированных или чисто стохастических задач), ввиду неопределенности значений вектора ypr. Она превратится в целевую функцию, если зафиксировать некоторое сочетание информации Уs, или другими словами, – однозначно определить условия создания и адаптации, однако полученный при этом оптимальный вариант решения Xs будет, лишь «локально-оптимальным» - наилучшим только для данных условий. Другим сочетаниям информации будут соответствовать иные локально-оптимальные варианты, и их совокупность не может считаться решением задачи. При известном вероятностном описании вектора ypr в качестве целевой функции может рассматриваться математическое ожидание функции З(xpr,ypr). Однако, в условиях неопределенности отсутствует и эта возможность. Поэтому, здесь она служит лишь для количественной оценки эффекта (с точки зрения главной цели) и будет называться «оценочной» функцией, при этом необходимо стремиться сделать ее значения как можно меньше или больше в зависимости от смысла, решаемой задачи.
Наиболее известная общая схема принятия решения в условиях неопределенности приведена на рисунке 5.3.
Первый этап связан с математической формулировкой задачи.
 Второй этап - выбор представительного множества сочетаний исходных данных, имеющих неоднозначный характер, - представляет собой фактически «дискретизацию» задачи в отношении вектора ypr, путем выявления существенных отличий во временных и стоимостных факторах. Формально речь идет об отборе нескольких (S) его значений, которые будут рассматриваться при последующем решении задачи. Как правило S не должно быть очень большим, так как для каждого сочетания информации (s=1,...,S) выполняется значительный объем вычислений. Поэтому важно
Второй этап - выбор представительного множества сочетаний исходных данных, имеющих неоднозначный характер, - представляет собой фактически «дискретизацию» задачи в отношении вектора ypr, путем выявления существенных отличий во временных и стоимостных факторах. Формально речь идет об отборе нескольких (S) его значений, которые будут рассматриваться при последующем решении задачи. Как правило S не должно быть очень большим, так как для каждого сочетания информации (s=1,...,S) выполняется значительный объем вычислений. Поэтому важно
Рис. Схема принятия решения в условиях неопределенности
при ограниченном числе S наиболее полно охарактеризовать ситуацию в целом.
Третий этап имеет двоякое назначение. С одной стороны, здесь выявляются те варианты xpr, которые в принципе могут оказаться рациональными и, поэтому должны подробно исследоваться. В этом отношении важно не пропустить «хорошие варианты». С другой стороны, на данном этапе проверяется, имеется ли в рассматриваемой ситуации неопределенность выбора, т.е. приводит ли неопределенность исходной информации к неопределенности решения. Если последней неопределенности нет, то решение задачи заканчивается - выявленный единственный оптимальный вариант принимается к исполнению. Если же неопределенность решения установлена, то проводится анализ для отбора конкурирующих вариантов (i=1,...,I), которые будут рассматриваться на последующих этапах. При выполнении данного этапа, так или иначе, приходится рассматривать возможные сочетания исходных данных (штриховая линия из блока 2 в блок 3).
Четвертый этап - расчет платежной матрицы - один из наиболее трудоемких в вычислительном отношении. Здесь для каждого оставленного для рассмотрения варианта решения (i=1,...,I) оценивается эффект при всех отобранных сочетаниях исходных данных (s=1,...,S), т.е. рассчитывается I´S значений оценочной функции З(xpr,ypr). Платежная матрица (таблица 5.1) необходима для корректного сопоставления конкурирующих вариантов сети. С одной стороны, из-за неоднозначности исходных данных приходится рассматривать несколько (S) их сочетаний. С другой стороны, для того чтобы можно было сопоставлять варианты xpri между собой, требуется оценивать эффект каждого при одних и тех же, т.е. фактически при всех, S сочетаниях информации. Без платежной матрицы просто невозможно провести правильное и полное сравнение решений в условиях неопределенности, поэтому предыдущие этапы в известном смысле являются подготовительными для данного четвертого этапа. Платежная матрица ||Зis|| дает количественную характеристику ситуации и служит основой для последующего анализа и выбора рациональных вариантов сети.
Таблица
Платежная матрица (значения оценочной функции)
| Вариант решения | Сочетание исходных данных | |||||
| ypr1 | ypr2 | … | yprs | ... | yprS | |
| xpr1 | З11 | З12 | З1s | З1S | ||
| xpr2 | З21 | З22 | З2s | З2S | ||
| : | ||||||
| xpri | Зi1 | Зi2 | Зis | ЗiS | ||
| : | ||||||
| xprI | ЗI1 | ЗI2 | ЗIs | ЗIS |
На этом пятом этапе используются специальные критерии и приемы теории решений, учитываются интуитивные представления о возможных вероятностях отобранных сочетаний исходных данных и т.д.. Иногда в ходе анализа выявляется один вариант решения, который можно достаточно уверенно рекомендовать для реализации. Это происходит, например, если все применяемые критерии выбора решений (Лапласа, Вальда, Севиджа и другие) указывают на один и тот же вариант или когда при всех вероятностных характеристиках, намеченных интуитивно, математическое ожидание оценочной функции З(xpr,ypr) оказывается наименьшим или, наоборот, наибольшим (в зависимости от смысла задачи) при одном и том же варианте решения (штриховая линия из блока 5 в блок 6).
Последний, шестой этап - окончательный выбор варианта решения корпоративной функционально-ориентированной сети, принимаемый к исполнению (будет рассматриваться более подробно).
Участие человека предполагается на все этапах, кроме четвертого.
Для анализа платежной матрицы можно определить и использовать некоторые характерные оценки вариантов. Наиболее интересные из них: максимальные для данного варианта затраты, минимальные затраты, среднеарифметические затраты, максимальное значение риска. Критериями выбора решений в условиях неопределенности являются: критерий Вальда, критерий Лапласа, Севиджа и критерий Гурвица. В условиях стохастической неопределенности ясно, что выбор того или иного подхода к принятию решения или критерия является субъективным. Поэтому, может оказаться полезным проанализировать ситуацию с точки зрения нескольких критериев выбора. Для этого можно сконструировать обобщенный критерий, в котором используются все характерные оценки вариантов. Наиболее просто и естественно минимизировать их линейную комбинацию. Очевидно, что такой критерий выбора решений имеет все недостатки предыдущих критериев и не снимает неопределенности выбора (он увеличивает число рациональных вариантов) и позволяет не упустить из внимания такие варианты, которые, не будучи оптимальными ни по одному из частных критериев, достаточно хороши по всей совокупности характерных оценок и могут оказаться более приемлемыми для реализации.
После того, как рассчитана платежная матрица, определение характерных оценок конкурирующих вариантов и различные манипуляции с ними не требуют больших вычислений и при определенном навыке разработчика сети не вызывают каких-либо трудностей. Для условий «частичной» неопределенности, когда разработчик сталкивается не с полным отсутствием вероятностного описания вектора ypr, а с неточностью (неоднозначностью) описания вместо платежной матрицы анализируется матрица математических ожиданий оценочной функции.
ВЫБОР БАЗОВОГО ВАРИАНТА СЕТИ
Среди существующих методов для задачи выбора базового варианта сети целесообразно выделить метод анализа иерархий. Этот метод является систематической процедурой для иерархического представления элементов, определяющих суть любой проблемы, и в частности проблемы выбора базового варианта корпоративной сети.
Преимущества метода анализа иерархий:
- метод дает возможность провести декомпозицию и анализ проблемы оценивания альтернативных решений в конкретной ситуации при создании и адаптации сети;
- позволяет учитывать предпочтения разработчика на множестве критериев, от него требуется лишь определить важность критерия путем попарного сравнения (эта процедура относится к классу нормально допустимых процедур по сложности);
- иерархическое представление системы принятия решений дает разработчику сети наглядную и простую для понимания картину влияния изменения приоритетов на верхних уровнях на приоритеты элементов нижних уровней;
- иерархии обладают свойством устойчивости и гибкости в том смысле, что расширение хорошо структурированной иерархии не разрушает ее характеристик, т.е. малые изменения вызывают малый эффект;
- с математической точки зрения он легко реализуем, а время работы программы определяется только продолжительностью начального диалога разработчика сети с ЭВМ.
Существует несколько видов иерархий. Для принятия концептуального (базового) решения о сети в процессе ее создания и адаптации наиболее приемлемыми являются доминантные иерархии. При выборе базового решения сети имеется набор альтернатив Х1, Х2, …, Хn и набор критериев оценки альтернатив К1,К2,…,Кk. Задача состоит в том, чтобы выбрать оптимальную альтернативу с учетом критериев оценки. В этом случае метод анализа иерархий можно разбить на 4 этапа.
1 этап. Построение множества матриц парных сравнений для всех уровней и групп, т.е. методом попарных сравнений необходимо оценить важность критериев. На данном этапе необходимо участие разработчика сети. Используя некоторую шкалу градации качества, он должен сравнить попарно все альтернативы и дать им оценку. Данная процедура относится к классу нормально-допустимых по сложности для пользователя.
При сравнении критериев попарно, получается матрица:
| К1 | … | Кi | … | Kv | ||
| К1 | x11 | … | x1i | … | x1v | |
| … | … | … | … | … | … | |
| Кj | xj1 | … | xji | … | xjv | |
| … | … | … | … | … | … | |
| Кv | Xv1 | … | Xvi | … | Xvk |
Необходимо заполнить часть матрицы, расположенной над главной диагональю, а другую часть вычислить. Матрица имеет свойства обратной симметричности, то есть xij=1/xji.
2 этап. На втором этапе вычисляются веса критериев:
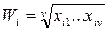 ,
,
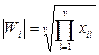 ,
,
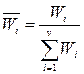 .
.
В результате будут получены веса критериев 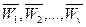 , или вектор локальных приоритетов критериев.
, или вектор локальных приоритетов критериев.
3 этап. Фиксируя каждый из критериев, надо сравнить важность альтернатив по ним. Данная процедура также относится к классу нормально-допустимых по сложности.
| Кi | Хi | … | Хn | |
| Х1 | y11 | … | y1n | |
| … | … | … | … | |
| Хn | yn1 | … | ynn |
4 этап.Вычисление весов альтернатив по каждому критерию:
Vl(Ki) = 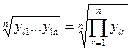 ,
,
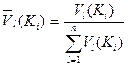 .
.
В результате получается матрица весов альтернатив по каждому критерию.
| Х1 | Х2 | … | Хn | |
| K1 | _ V1(K1) | _ V2(K1) | … | _ Vn(K1) |
| … | … | … | … | … |
| Kv | _ V1(Kv) | _ V2(Kv) | … | _ Vn(Kv) |
На этом же этапе вычисляются функции ценности для каждой альтернативы.
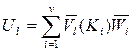 .
.
После этого по функции ценности выбирается оптимальная альтернатива (базовое или концептуальное решение сети) в условиях неопределенности исходной информации.
Дата добавления: 2016-02-13; просмотров: 879;
