Преобразование частоты
Преобразование- это изменение (сдвиг) частоты сигнала.
Преобразование часто используется в радиоприемных устройствах для понижения частоты.
Обычно для преобразования частоты используют усилитель с нелинейной характеристикой, на вход которого подается сигнал преобразуемой частоты (w0) и сигнал вспомогательного генератора частотой wг. Нагрузкой усилителя является колебательный контур с резонансной частотой равной w0+wг либо wг-w0.

Благодаря нелинейности в спектре коллекторного тока появляются гармонические и комбинационные частоты. На одну из комбинационных частот (например wг-w0) настроен колебательный контур.
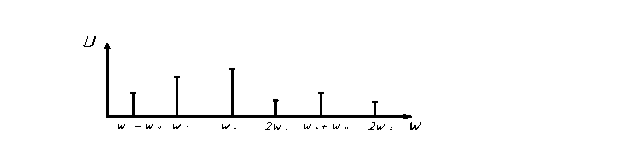 На колебательном контуре выделяется лишь напряжение, создаваемое составляющей коллекторного тока с частотой Wг-W0 .
На колебательном контуре выделяется лишь напряжение, создаваемое составляющей коллекторного тока с частотой Wг-W0 .
Если заданная частота исходного сигнала W0 и частота сигнала, которую необходимо получить (Wпр.- промежуточную), то частоту вспомогательного генератора Wг выбирают из условия Wг=Wпр+ W0 либо Wг=Wпр- W0 .
При преобразовании частоты необходимо обеспечить наибольшую амплитуду комбинационных частот.
Математический анализ показывает что амплитуды комбинационных частот пропорциональны амплитудам преобразуемого сигнала и сигнала вспомогательного генератора:
i(t)= a0+a1U+a2 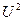

U(t)=(Uмгsinwгt+Uмсsinwct)
a2 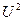 =a2Uмг
=a2Uмг 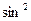 wгt+a2Umc
wгt+a2Umc 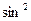 wct+2a2UмгUmcsinwгt*sinwct
wct+2a2UмгUmcsinwгt*sinwct
2a2UмгUmcsinwгt*sinwct=a2UмгUmc*cos(wг-wc)t- a2UмгUmccos(wг-wc)
т.е амплитуды комбинационных частот зависит от а2UмгUmc в свою очередь коэффициент а2 зависит от амплитуд Uмг и Umc и от формы ВАХ. От амплитуд а2 зависит величина нелинейного участка ВАХ, а значит степень нелинейности.
В отличии от усилителей в преобразователях амплитуды Uмг и Umc могут быть достаточно большими, поэтому в качестве преобразователя можно использовать обыкновенный п/п диод, имеющий такую же ВАХ, как и транзистор. 
Детектирование
Детектирование предназначено для выделения НЧ сигнала из модулируемого сигнала.
1. Детектирование АМ сигналов.
Детектирование АМ сигнала можно осуществить с помощью нелинейного элемента, например диода При этом различают 2 основных режима: квадратичный и линейный.
а) Квадратичный режим детектирования.
Если амплитуда детектируемого напряжения мала и не выходит за пределы криволинейного квадратичного участка, то режим называется квадратичным и выходной ток описывается полиномом 2-ой степени:
i(t)= a0+a1U+a2U 
Для модулирования АМ колебания:
U(t)=(Umw+Um 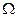 sin
sin 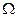 t)sinwt ,тогда:
t)sinwt ,тогда:
i(t)=a0+a1(Umw+Um 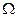 sin
sin 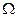 t)sinwt+a2(Umw+Umsin
t)sinwt+a2(Umw+Umsin 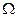 t)
t) 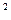 sin
sin 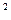 wt
wt
Произведение во втором слагаемом дает слагаемые с частотой w- 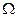 и w+
и w+ 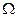 , которые много больше чем
, которые много больше чем 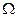 и легко отфильтровуются ФНЧ.
и легко отфильтровуются ФНЧ.
a2(Umw+Um 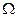 sin
sin 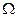 t)
t) 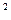 sin
sin 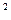 wt=a2 U
wt=a2 U  mw sin
mw sin 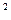 wt+a2U
wt+a2U  m
m 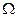 sin
sin 
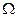 t* sin
t* sin 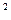 wt+2a2Umw Um
wt+2a2Umw Um 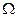 *sin
*sin 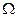 t* sin
t* sin 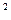 wt
wt
Анализ показывает, что в спектре выходного тока кроме нелинейных частот присутствуют слагаемые с частотой 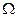 и 2
и 2 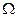 , причем амплитуда слагаемого с частотой
, причем амплитуда слагаемого с частотой 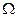 в 4 раза больше чем амплитуда слагаемых с частотой 2
в 4 раза больше чем амплитуда слагаемых с частотой 2 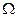 (при m=1). Отфильтровать частоту 2
(при m=1). Отфильтровать частоту 2 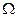 невозможно, но ввиду широкого спектра НЧ сигнала т.е спектры перекрываются.
невозможно, но ввиду широкого спектра НЧ сигнала т.е спектры перекрываются. 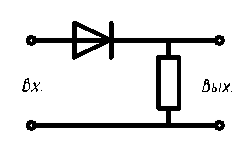
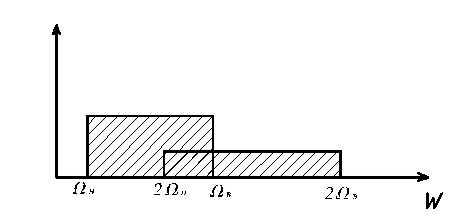
Большая амплитуда второй гармоники приводит к сильным искажениям (до 25% при m=1 до 10% при m=0.3).
б) Линейный режим детектирования.
Если амплитуда детектируемого напряжения достаточно велика и занимает большую часть линейного участка ВАХ, то режим называется линейным (считается линейным ввиду того, что применение амплитуды происходит главным образом на линейном участке ВАХ).
Амплитуды гармоник зависят от амплитуд импульсов и угла отсечки. При неизменном 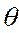 (
( 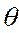 =90
=90 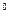 ) амплитуды гармоник (в том числе нелинейная составляющая зависит только от амплитуды импульсов).
) амплитуды гармоник (в том числе нелинейная составляющая зависит только от амплитуды импульсов).
I0= 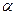 0imax
0imax
В свою очередь амплитуда сигналов линейно зависит от амплитуды модулированного напряжения, которое изменяется по закону sin 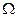 t. Для выделения постоянной составляющей (медленно меняющейся) или ФНЧ.
t. Для выделения постоянной составляющей (медленно меняющейся) или ФНЧ.
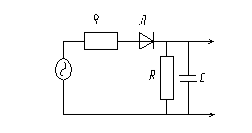
ФНЧ состоит из (RГ+RД) и С. Резистор R нужен для того чтобы конденсатор разряжался через него при уменьшении амплитуд импульсов.
В противном случае диод оказался бы запертым и детектор не отслеживал бы изменения амплитуды импульсов в сторону уменьшения.
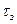 =(Rг+Rд)С
=(Rг+Rд)С
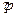 =R*R;
=R*R; 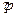 >
> 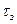
Дата добавления: 2016-03-15; просмотров: 1178;
