Системы M/G/1 с перерывами
Пусть T1,T2,… - продолжительности последовательных перерывов, которые делает обслуживающий прибор и T1,T2,… - независимые одинаково распределенные случайные величины, которые также не зависят от интервалов между моментами поступления запросов и длительностей их обслуживания. Моменты поступления образуют пуассоновский поток, а длительности обслуживания являются независимыми и имеют произвольное распределение. Вновь поступивший в систему запрос должен ждать в очереди завершения обслуживания текущего запроса или завершения перерыва, а затем должен ждать, пока будут обслужены все запросы, стоящие перед ним. Таким образом, выполняется равенство
MOW = 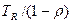 ,
,
где TR - среднее остаточное время для завершения обслуживания или перерыва в момент, когда поступает i-й запрос.
Если М(t) - число обслуживаний, которые завершились к моменту t , a L (t) - число перерывов, которые закончились к моменту t, то для любого момента t,когда точно завершается обслуживание или перерыв справедливо выражение:
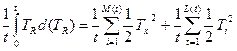 .
.
Предполагается, что среднее по времени можно заменить на среднее по вероятности и получить, что 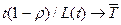 при возрастании t, где
при возрастании t, где 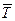 и
и 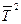 — первый и второй моменты длительности перерыва соответственно.
— первый и второй моменты длительности перерыва соответственно.
Тогда, учитывая, математическое ожидание времени, проведенного в очереди в системе M/G/1с перерывами равно:
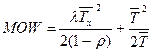 .
.
Дата добавления: 2016-02-13; просмотров: 672;
