Система М/М/M/M с потерями и с Т обслуживающими приборами

Эта система подобна системе М/М/т за исключением того, что, если запрос при поступлении в систему обнаружит, что все т обслуживающих приборов заняты, он не поступит в систему, а потеряется, эта модель широко применяется в телефонии. В корпоративных компьютерных сетях такая модель может использоваться для исследования сети, в которой моменты поступления соответствуют заявкам на установление виртуальных соединений между двумя узлами, а максимально возможное число виртуальных связей равно т. Средняя длительность обслуживания 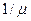, в этом случае равна среднему времени использования виртуального соединения.

Пусть 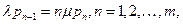так, что 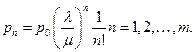Тогда, с учетом равенства 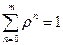получается:

.

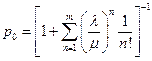Система M/G/1

Можно проанализировать СМО с одной очередью, в которой запросы поступают в соответствии с пуассоновским процессом с интенсивностью 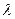, но длительности обслуживания имеют произвольное распределение, не обязательно экспоненциальное, как в системе М/М/1. Запросы обслуживаются в порядке поступления, T_xi - длительность обслуживания i-го запроса, случайные величины (T_x1,T_x2,…) одинаково распределены, взаимно независимы и не зависят от интервалов между моментами поступления.

Пусть 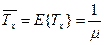- средняя длительность обслуживания, 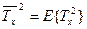- второй момент длительности обслуживания. Из формулы Поллячека — Хинчина:

,

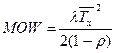где MOW - математическое ожидание времени пребывания запроса в очереди, а .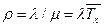

Общее время пребывания в очереди и в обслуживающем приборе равно

.

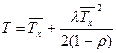Применяя формулу Литтла для MOW и Т, можно получить математическое ожидание числа запросов в очереди MO 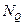и математическое ожидание числа запросов в системе:

.

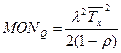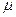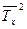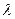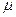Так как в случае M/D/1 при данном получается минимально возможное значение , из этого следует, что при одинаковых значениях и величины MOW, T, MO_Q и N для системы массового обслуживания M/D/1 являются нижними границами для соответствующих величин в системе M/G/1. Необходимо заметить, что MOW и MO 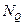для системы M/D/1 равны половине их значений в системе М/М/1. Вместе с тем значения Т и N при малых 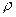для M/D/1такие же, как в системе М/М/1, и приближаются к половине их значений в системе М/М/1 по мере того, как 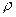приближается к 1. Дело в том, что математическое ожидание длительности обслуживания одно и то же в обоих случаях и при малых 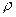большую часть времени пребывания в системе запросы находятся в обслуживающем приборе, а при больших 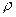большую часть времени ожидают в очереди.