Распределение числа запросов

Если поступления запросов являются нетипичными и стационарные вероятности их числа в момент поступления -

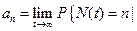запрос поступил сразу же после момента t},

необязательно равны соответствующим безусловным стационарным вероятностям

,

но для системы М/М/1:

,

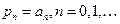тогда, для любого момента t и длины интервала 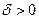число запросов, поступивших в интервале 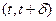, не зависит от числа запросов, находящихся в системе в момент t. При использовании свойств пуассоновского процесса это эквивалентно предположению, что в любой момент времени длительность обслуживания поступивших ранее запросов и интервалы между будущими моментами поступлений являются независимыми, до некоторой степени это выполняется и в сетях пакетной передачи. Такое предположение справедливо, если процесс поступления является пуассоновским, а интервалы между моментами поступления и длительности обслуживания независимы.

Равенство 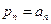, выполняется, так как, по предположению, события 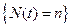(запрос поступил сразу же после момента t) независимы. В результате условная вероятность будет равна безусловной.

Пусть 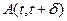соответствует событию, что запрос поступает в интервале 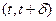и

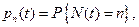
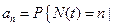запрос поступает сразу же после момента t}.

Используя формулы Байеса можно получить, что:

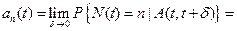
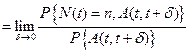
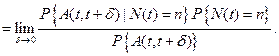
По предположению событие 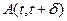не зависит от числа запросов, находящихся в системе в момент t. Следовательно

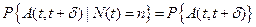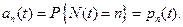: , а для 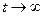будет получена формула. Таким образом, если процесс поступления запросов пуассоновский, то поступивший в систему запрос определяется обычным состоянием.

При распределении числа запросов в системе сразу же после того, как запрос покидает систему, вероятность равна:

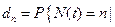запрос поступает непосредственно перед моментом t}.

Соответствующие стационарные вероятности можно обозначить как 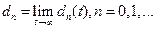. При очень общих предположениях 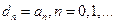- система достигала стационарного состояния, в котором стационарные вероятности положительны при всех п, и число запросов N(t) имеет приращения, равные единице. Для любого увеличения состояния системы от п до п+1 из-за поступления нового запроса в дальнейшем будет соответствующее уменьшение от n+1 до п из-за ухода запроса из системы. Следовательно, при длительной работе доля переходов из п в п+1 среди общего их числа из любого k в k+1 равна доле переходов из п+1 в п среди всех переходов из любого k+1 в k,а 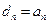, и в стационарном состоянии для поступающего и уходящего запроса система выглядит как статистически одинаковая.