Система М/М/M с M обслуживающими приборами
Уравнения равновесия для стационарных вероятностей 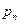 при
при 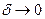 можно записать следующим образом:
можно записать следующим образом:
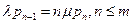 ,
, 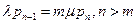 .
.
Из этих уравнений следует, что:
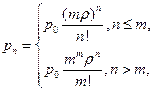
где 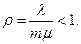
Можно вычислить 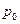 , используя формулу и условие
, используя формулу и условие 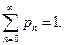 Тогда:
Тогда:
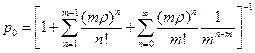 , и окончательно
, и окончательно
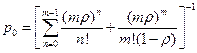 .
.
Вероятность того, что поступивший запрос обнаружит в системе, что все обслуживающие приборы заняты, и будет поставлен в очередь для ожидания, равна
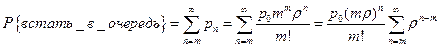 ,
,
следовательно,
PQ □ P {встать в очередь}= 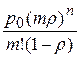 ,
,
где PQ можно определить из формулы Эрланга.
Математическое ожидание числа запросов, находящихся в очереди равно: MO 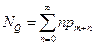 .
.
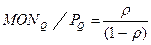 дает условное математическое ожидание числа запросов, ожидающих в очереди при поступлении запроса, при условии, что этот запрос направляется в очередь для ожидания. Математическое ожидание при заданном
дает условное математическое ожидание числа запросов, ожидающих в очереди при поступлении запроса, при условии, что этот запрос направляется в очередь для ожидания. Математическое ожидание при заданном 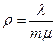 не зависит от числа обслуживающих приборов. Оно указывает, в частности, на то, что, если имеются запросы, ожидающие в очереди, длина очереди в системе М/М/т ведет себя так же, как в системе М/М/m со скоростью обслуживания
не зависит от числа обслуживающих приборов. Оно указывает, в частности, на то, что, если имеются запросы, ожидающие в очереди, длина очереди в системе М/М/т ведет себя так же, как в системе М/М/m со скоростью обслуживания 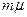 , равной суммарной скорости т обслуживающих приборов.
, равной суммарной скорости т обслуживающих приборов.
Следовательно, средняя задержка в системе равна
tз.ср = 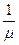 + tож =
+ tож = 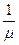 +
+ 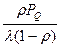 ,
,
и среднее число запросов в системе составляет
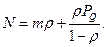
Дата добавления: 2016-02-13; просмотров: 699;
