Алгоритм цифровой подписи EC-DSA.

Алгоритм DSA можно обобщить на произвольную конечную абелеву группу A , в которой сложно решается задача дискретного логарифмирования, порождающий элемент G имеет простой порядок Q > 2¹⁶⁰ и существует открытая функция F: A ® Z/QZ. В последнее время широкое распространение получили криптосистемы на эллиптических кривых. Аналог алгоритма DSA обобщенный для работы с эллиптическими группами точек носит название EC-DSA.

Различия в средах оперирования DSA и EC-DSA сведены в таблицу

Таблица 16. Параметры DSA и EC-DSA.

Параметр	DSA	EC-DSA
А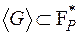
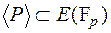
G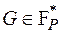
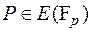
Y	Gx	[x]P
F	(mod Q)	x-координата по модулю Q

В обобщенной версии DSA каждый пользователь тоже генерирует секретный подписывающий ключ x и вычисляет открытый по формуле: Y = [x]P. Подпись получается в результате выполнения следующего алгоритма:

- Вычисляется хэш-значение H = H(M).

- Выбирается эфемерный ключ k, 0 < k < Q.

- Определяется R = F([k]P) и S = (H + xR)/k (mod Q).

Подписью сообщения M служит пара (R, S).

Для проверки подписи (R, S) на сообщении M осуществляют следующую процедуру:

- Вычисляют хэш-значение H = H(M).

- Определяют A = H/S (mod Q) и B = R/S (mod Q).

- Находят V = F([A]P + [B]Y), где Y – открытый ключ подписавшего сообщение.

- Подпись считается корректной, если V = R.

Пример. Возьмем за основу эллиптическую кривую над полем F₁₉₉ вида:

E: Y ² = X ³ + X + 3.

Число ее элементов равно Q = 197, то есть является простым. Поэтому соответствующая группа – циклическая, а координаты ее образующей P – (1, 76). Выберем x = 29 в качестве закрытого ключа. Тогда соответствующий открытый ключ будет равен

Y = [x]P = [29](1, 76) = (113, 191).

Предположим, что владелец закрытого ключа намерен подписать сообщение с хэш-значением H(M) = 68. Тогда ему нужно сгенерировать эфемерный ключ, который выберем k = 153, и вычислить

R = x-коорд.([k]P) = x-коорд.([153](1, 76)) = x-коорд.((185, 35)) = 185.

Далее он находит

S = (H(M) + x · R)/k (mod Q) = (68 + 29 · 185)/153 (mod 197) = 78.

Подпись, которую он посылает вместе с сообщением, - это пара (R, S) = (185, 78).

Чтобы проверить подпись, мы вычисляем

A = H(M)/S (mod Q) = 68/78 (mod 197) = 112,

B = R/S (mod Q) = 185/78 (mod 197) = 15.

После этого определяем

Z = [A]P + [B]Y = [112](1, 76) + [15](113, 191) = (111, 60) + (122, 140) = (185, 35).

Подпись оказалась верной, поскольку

R = 185 = x-коорд.(Z).