Проективные координаты.
Одна из проблем, возникающих при использовании формул группового закона как при большой, так и при четной характеристике поля, связана с необходимостью деления. Деление в конечном поле считается дорогой операцией, так как включает в себя некий вариант расширенного алгоритма Евклида, который хотя и имеет приблизительно ту же сложность, что и умножение, однако обычно не может быть реализован достаточно эффективно.
Во избежание операции деления применяют проективные координаты. При этом уравнение кривой записывается через три координаты (X, Y, Z) вместо двух (X, Y). Однако вместо стандартного варианта уравнения кривой используется уравнение вида
E: Y2 + a1XYZ + a3YZ4 = X3 + a2X2Z2 + a4XZ4 + a6Z6.
Точка на бесконечности здесь также имеет координаты (0, 1, 0), но переход от аффинных координат к проективным осуществляется по правилу
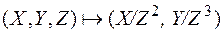 .
.
выбор таких координат обусловлен стремлением сделать арифметические операции более эффективными.
Сжатие точек.
Во многих криптографических протоколах возникает необходимость хранить в памяти или передавать по сети отдельные точки эллиптической кривой. В аффинных координатах это можно сделать при помощи двух элементов поля: координат x и y. Однако экономнее применять так называемую технику сжатия точек.
Метод сжатия точек работает благодаря тому, что уравнение кривой в аффинных координатах при фиксированном значении x превращается в квадратно уравнение относительно координаты y. Значит, вместо двух координат для идентификации точки кривой можно хранить в памяти компьютера только координату x и еще некий двоичный параметр b, сообщающий о том, какое именно значение координаты y нужно брать.
Кривые над полем характеристикиp > 3
Пусть основное поле K = Fq с q = pn, где p > 3 – простое число и 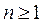 .
.
Уравнение кривой над таким полем можно представить в виде короткой формы Вейерштрасса
E: Y2 = X3 + aX + b.
Ее дискриминант равен Δ = – 16(4a3 + 27b2), а j-инвариант – j(E) = – 1728(4a)3/ Δ.
Формулы группового закона: – P1 = (x1, y1) и, если P3(x3, y3) = P1 + P2 ¹ O, то координаты x3, y3 вычисляются так:
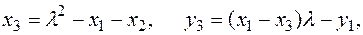
где при x1 ¹ x2
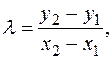
а при x1 = x2, y1 ¹ 0
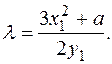
В проективных координатах формулы сложения точек эллиптической кривой, заданной уравнением
E: Y2 = X3 + aXZ2 + bZ6,
над полем характеристики p > 3 выглядят как
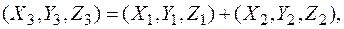
где тройка координат 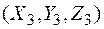 вычисляется последовательно по правилу:
вычисляется последовательно по правилу:
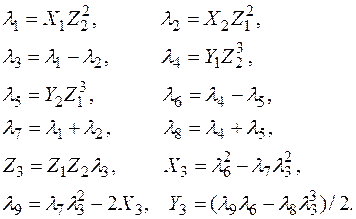
здесь нет ни одной операции деления, кроме деления на 2, которое легко заменяется умножением на заранее вычисленное число 2–1(mod p).
Удвоение точек 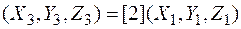 упрощается с помощью формул
упрощается с помощью формул
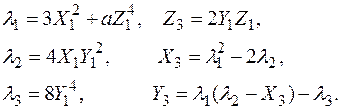
Сжатие точек эллиптической кривой над полем характеристики p > 3.
Если p > 2, то квадратные корни ± β из элемента α Î Fp представляются натуральными числами разной четности из промежутка 1, …, p – 1, поскольку
– β=p – β (mod p).
Таким образом в качестве параметра b можно выбрать четность y координаты соответствующей точки. Полная информация о координатах точки по паре (x, b) осуществляется следующим образом. Сначала вычисляется
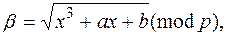
а затем переменной y присваивают значение β, если четность β совпадает с четностью b, и p – β, когда четности разные. Если же оказывается, что β = 0, то, не обращая внимания на параметр b, можно положить y = 0.
Не путать параметр четности b с коэффициентом кривой b.
Эллиптические группы.
Эллиптическая группа по модулю p определяется следующим образом. Выбираются два неотрицательных числа a и b, которые меньше p и удовлетворяют условию
4a3 + 27b2 (mod p) ¹ 0 (кривая не аномальная и не суперсингулярная).
Тогда Ep(a, b) обозначает эллиптическую группу по модулю p, элементами которой (x, y) являются пары неотрицательных целых чисел, которые меньше p и удовлетворяют условию
y2 ≡ x3 + ax + b (mod p)
вместе с точкой в бесконечности O.
Пример.
p = 23. Рассмотрим эллиптическую кривую y2 = x3 + x + 1. В этом случае a = b = 1 и мы имеем 4 ´ 13 + 27 ´ 12 (mod 23) = 8 ¹ 0, что удовлетворяет условиям эллиптической группы по модулю 23.
Для эллиптической группы рассматриваются только целые значения от (0, 0) до (p, p) в квадранте неотрицательных чисел, удовлетворяющих уравнению по модулю p.
В общем случае список таких точек (см. табл.) составляется по следующим правилам.
1. Для каждого такого значения x, что 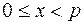 , вычисляется x3 + ax + b (mod p).
, вычисляется x3 + ax + b (mod p).
2. Для каждого из полученных на предыдущем шаге значений выясняется, имеет ли это значение квадратный корень по модулю p (вычисляется символ Лежандра). Если нет, то в Ep(a, b) нет точек с этим значением x. Если же корень существует, имеется два значения y, соответствующих операции извлечения квадратного корня (исключением является случай, когда единственным таким значением оказывается y = 0). Эти значения (x, y) и будут точками Ep(a, b).
Таблица 15. Точки на эллиптической кривой E23(1, 1)
| (0, 1) | (1, 7) | (3, 10) | (4, 0) | (5, 4) | (6, 4) | (7, 11) |
| (0, 22) | (1, 16) | (3, 13) | O | (5, 19) | (6, 19) | (7, 12) |
| (9, 7) | (11, 3) | (12, 4) | (13, 7) | (17, 3) | (18, 3) | (19, 5) |
| (9, 16) | (11, 20) | (12, 19) | (13, 16) | (17, 20) | (18, 20) | (19, 18) |
Пример. Сложение и удвоение точек данной группы. P = (3, 10), Q = (9, 7).
Сложение:
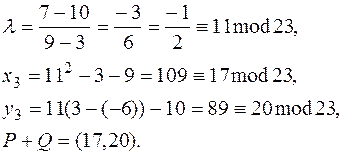
Удвоение:
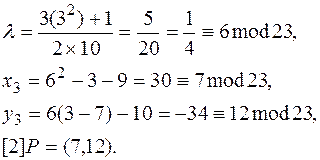
Умножение определяется как повторное применение операции сложения
[4]P = P + P + P + P.
Дата добавления: 2016-02-13; просмотров: 2860;
