Эллиптические кривые.

Проективная плоскость P²(K) над полем K определяется как множество троек (X, Y, Z) не равных одновременно нулю элементов X, Y, Z Î K, на котором введено отношение эквивалентности:

(X, Y, Z) ~ (lX, lY, lZ) для любых l Î K^*.

Так, например, две точки (4, 1, 1) и (5, 3, 3) эквивалентны в P²(F₇).

Класс эквивалентности троек называется проективной точкой.

Эллиптической кривой E называется множество точек проективной плоскости, удовлетворяющих однородному уравнению Вейерштрасса

E: F(X, Y, Z) = –X³ + Y²Z + a₁XYZ – a₂X²Z + a₃YZ² – a₄XZ² – a₆Z³ = 0,

c a_i Î K.

Это уравнение называют также длинной формой Вейерштрасса. Кривая должна быть неособой в том смысле, что частные производные 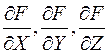не должны обращаться в нуль одновременно ни в одной ее точке.

Множество K-рациональных точек кривой E (то есть точек, удовлетворяющих уравнению кривой) обозначается через E(K).

Кривая имеет только одну точку, чья координата Z = 0, а именно (0, 1, 0). Ее принято называть бесконечно удаленной точкой (или точкой на бесконечности) и обозначать символом O.Для удобства часто пользуются аффинной версией уравнения Вейерштрасса:

E: Y² + a₁XY + a₃Y = X³ + a₂X² + a₄X + a₆, c a_i Î K.

K-рациональные точки в аффинном случае – это решения уравнения в K² и бесконечно удаленная точка O.

Переход от аффинных к проективным координатам:

- точка на бесконечности всегда переходит в бесконечно удаленную точку, как при переходе от аффинных координат к проективным, так и наоборот;

- проективная точка (X, Y, Z) кривой, отличная от бесконечно удаленной (Z ¹ 0), переходит в аффинную точку с координатами (X/Z, Y/Z);

- чтобы найти проективные координаты аффинной точки (X, Y), не лежащей на бесконечности, достаточно выбрать произвольное значение Z Î K^* и вычислить (X·Z, Y·Z, Z).

Иногда удобнее пользоваться модифицированной формой проективной плоскости, когда проективные координаты (X, Y, Z) представляют аффинную точку (X/Z², Y/Z³).

Для эллиптической кривой вводятся следующие константы:

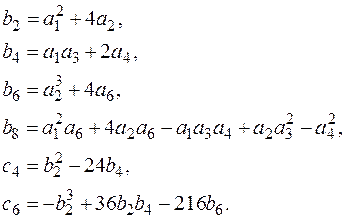
Дискриминант кривой E определяется по формуле

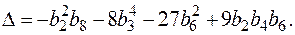
Если char K ¹ 2, 3, то дискриминант можно вычислить и так:

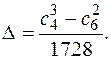
Деление на 1728 = 2⁶3³ имеет смысл только в тех полях, чья характеристика отлична от 2 и от 3. Кривая E неособа тогда и только тогда, когда 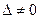. Далее рассматриваются только неособые кривые.

Для неособых кривых вводится j-инвариант

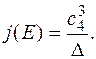
он тесно связан с понятием изоморфизма эллиптических кривых.

Говорят, что кривая E с координатами X и Y изоморфна над полем K кривой E’ с координатами X’, Y’ (обе заданы уравнением Вейерштрасса), если найдутся такие константы r, s, t Î K и u Î K^*, что при замене переменных

X = u²X’ + r, Y = u³Y’ + su²X’ + t

кривая E перейдет в кривую E’. Отметим, что изоморфизм кривых определен относительно поля K. Изоморфизм эллиптических кривых является отношением эквивалентности.

Лемма. Изоморфные над полем K кривые имеют один и тот же j-инвариант. С другой стороны, любые кривые с совпадающими j-инвариантами изоморфны над алгебраическим замыканием 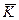поля K. То есть j-инвариант разделяет классы эквивалентности отношения изоморфизма над алгебраическим замыканием 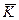поля K.

Групповой закон

Рассмотрим для char K ¹ 2, 3 замену переменных

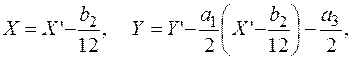
переводящую кривую заданную длинной формой Вейерштрасса в изоморфную ей кривую, определяемую короткой формой Вейерштрасса E: Y² = X³ + aX + b при некоторых a, b Î K. На таких представителях классов изоморфных эллиптических кривых можно наглядно ввести групповой закон методом хорд и касательных.

Сложение точек определяется с помощью хорд. Пусть P и Q – две точи кривой. Соединим их прямой линией. Она обязательно пересечет кривую в какой-то третьей точке R поскольку мы пересекаем кубическую кривую прямой. Точка R будет определена над тем же полем, что сама кривая и исходные точки P и Q. Отразим затем точку R относительно горизонтальной оси координат и получим точку, определяемую над основным полем. Последняя точка и будет суммой P + Q.

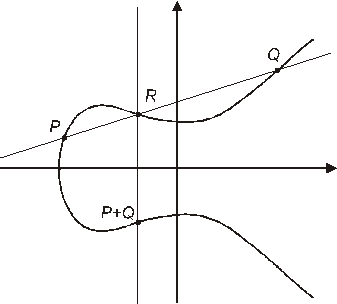
Рис.38. Групповой закон. Сложение точек.

Касательные служат для удвоения точек (используя хорду нельзя сложить точку с собой). Пусть P – произвольная точка эллиптической кривой. Проведем касательную к кривой в точке P. Она пересечет кривую в какой-то третьей точке R (кубическая кривая пересекается по трем точкам с учетом кратности пересечения). Отразив R относительно горизонтальной оси, мы получим точку [2]P = P + P. Вертикальная касательная в точке P «пересекает» кривую в бесконечно удаленной точке. В этой ситуации P + P = O и говорят, что P – точка порядка 2.

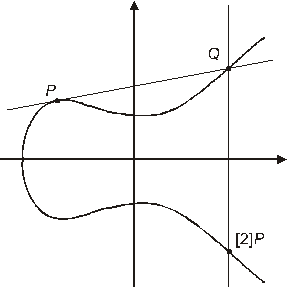
Рис.39. Групповой закон. Удвоение точек.

Метод хорд и касательных наделяет эллиптическую кривую структурой абелевой группы с бесконечно удаленной точкой в качестве нейтрального (единичного) элемента, то есть нуля. Определение операций можно легко перенести на случай общей эллиптической кривой, заданной длинной формой Вейерштрасса (в частности характеристика поля может быть любой). Необходимо только заменить отражение относительно оси абсцисс на симметрию относительно прямой

Y = a₁X + a₃

Алгебраические формулы, реализующие сложение точек по методу хорд и касательных.

Лемма. Пусть E – эллиптическая кривая, определяемая уравнением

E: Y² + a₁XY + a₃Y = X³ + a₂X² + a₄X + a₆,

на которой выбраны точки P₁(x₁, y₁) и P₂(x₂, y₂). Точка –P₁ имеет координаты

–P₁(x₁ – y₁ – a₁x₁ – a₃).

Введем коэффициенты

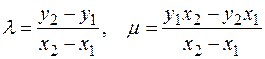
при x₁ ¹ x₂ и

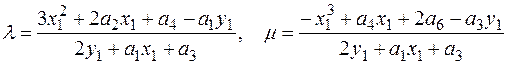
если x₁ = x₂, но P₂ ¹ –P₁. Если P₃(x₃, y₃) = P₁ + P₂ ¹ O, то x₃ и y₃ вычисляются по формулам:

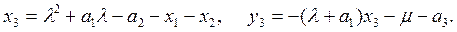
Фиксируем натуральное число m и обозначим через [m] отображение кривой на себя, сопоставляющее каждой точке P ее кратное [m]P, то есть

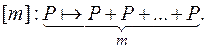
Это отображение – основа криптографических систем, опирающихся на эллиптическую кривую, поскольку его можно легко вычислить, но крайне сложно обратить, то есть по данным координатам P(x, y) и [m]P(x’, y’) найти m очень трудно. (Конечно сложность обращения предполагает специальный выбор эллиптической кривой и соблюдения других условий).