Возможные атаки на систему RSA.

1. Факторизация модуля n = p · q.

2. Решение сравнения 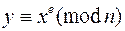для конкретного y - нахождение корня степени e из y по модулю p. (задача не менее сложная, чем задача факторизации).

3. Метод повторного шифрования – сводится к поиску ключа d’ для дешифрования на основе того, что существует такое натуральное число m, что 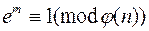. Производится последовательное повторное зашифрование сообщения y: 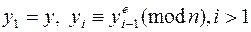до тех пор, пока не получим опять значения y: 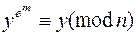, решением будет: x = y_m-1.(Метод эффективен при неправильном подборе параметров RSA.)

4. Метод факторизации модуля системы на основе дискредитированного ключа d. (Нельзя использовать одинаковый модуль для многопользовательских систем, при потере хотя бы одного ключа – вскрывается вся система.) Кроме того, знание хотя бы одного секретного ключа многопользовательской системы с единым модулем позволяет найти любой другой секретный ключ даже без факторизации n.

5. Определение секретного ключа d простым перебором (при малом d.)

6. Определение секретного ключа d с использованием непрерывных дробей, по теореме Винера (при .)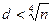

7. Бесключевое чтение циркулярных сообщений на общей открытой экспоненте e и трех взаимно простых модулях n₁, n₂, n₃ посредством решения системы из трех сравнений.