Кривые над полем характеристики 2

Пусть основное поле K = F_q с q = 2ⁿ при 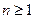. В этом случае j-инвариант кривой вычисляется по формуле 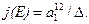Условие j(E) = 0, то есть a₁ = 0, в характеристике 2 равносильно суперсингулярности кривой E, а такие кривые в криптографии не используются поэтому полагаем что j(E) ¹ 0.

В этих предположениях представитель любого класса изоморфизма эллиптических кривых над F_q записывается уравнением

E: Y² + XY = X³ + a₂X² + a₆,

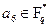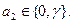где и Здесь γ – фиксированный элемент поля F_q, удовлетворяющий соотношению: .

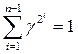Формулы группового закона: – P₁ = (x₁, y₁ – x₁) если P₃(x₃, y₃) = P₁ + P₂ ¹ O, то

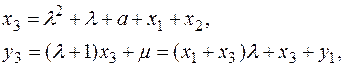
где при x₁ ¹ x₂

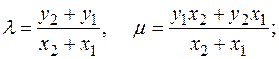
а при x₁ = x₂ ¹ 0

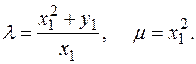
В проективных координатах формулы сложения точек эллиптической кривой, заданной уравнением

E: Y² + XYZ = X³ + a₂X²Z⁴ + a₆Z⁶,

над полем характеристики p = 2 выглядят как

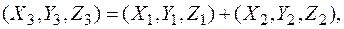
где тройка координат 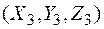вычисляется последовательно по правилу:

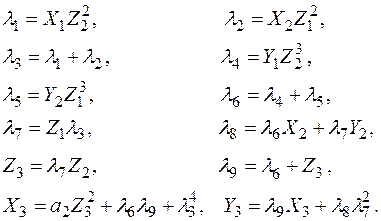
Координаты удвоенной точки 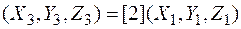определяются по правилу:

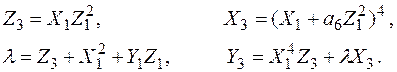
Сжатие точек эллиптической кривой над полем характеристики 2.

Дана точка P(x, y) на эллиптической кривой. Если y = 0, то можно положить b = 0. В противном случае вычисляют z = y / x и присваивают переменной b самый младший двоичный разряд числа z. Для восстановления y по данной паре (x, b) в случае x ¹ 0 вычисляют

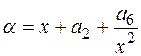
и обозначают через β одно из решений уравнения z² + z = α.

Если наименьший двоичный разряд числа β совпадает с b, то y = xβ. В противном случае y = x(β – 1).