Регрессионный анализ. Регрессионный анализ позволяет предсказать, чему в среднем будет равно значение одного признака при заданном значении другого признака.

Регрессионный анализ позволяет предсказать, чему в среднем будет равно значение одного признака при заданном значении другого признака.

Достаточно часто связь между двумя психологическими признаками имеет линейный характер:

у = a + bx, где

· y и x - анализируемые признаки;

· а - свободный член уравнения; при b = 0 получаем y = а, т.е. а - это точка, в которой линия регрессии пересекается с осью
OY (эту точку называют также «j-пересечением», или
«Intercept»);

· b - коэффициент регрессии, отражающий угол наклона
линии регрессии. Чем больше b отличается от 0, тем сильнее
связь между анализируемыми признаками.

Даже если связь между психологическими признаками носит нелинейный характер (например, экспоненциальный), практически всегда можно выделить участки, хорошо аппроксимируемые линейной регрессией.

Приведенное выше уравнение можно использовать для описания связи между двумя признаками лишь при выполнении следующих обязательных условий:

· зависимость между признаками носит линейный характер;

· оба признака распределены нормально.

Пример задачи: Исследователь должен определить коэффициенты линейного регрессионного уравнения, описывающего связь между показателями систолического давления и нервно-психической устойчивостью (НПУ) испытуемых.

Решение: Расчет коэффициентов регрессионных уравнений можно выполнить в нескольких модулях программы Statistica 6.0. Мы воспользуемся модулем Multiple Regression Analysis
(Анализ множественной регрессии).

В появившемся окне нажмите на кнопку Variables и укажите, какая из анализируемых переменных является зависимой (Dependent variable), а какая - независимой (Independent variable) (в нашем примере систолическое давление зависит от НПУ).

Нажмите на кнопку «ОК».

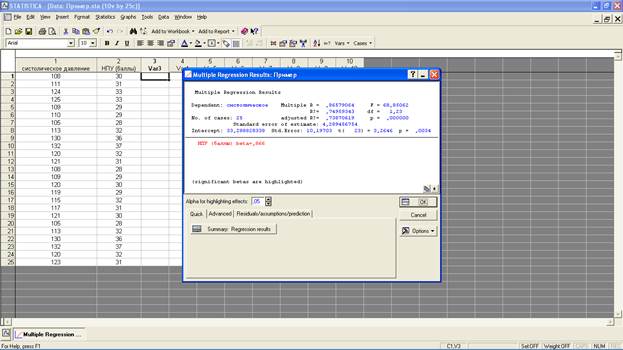
В итоге появится окно, которое уже на данном этапе анализа содержит некоторые важные его результаты:

а) Dependent: имя зависимой переменной;

б) No. of cases: число наблюдений;

в) Intercept: значение свободного члена регрессионного уравнения;

г) Std. error: стандартная ошибка свободного члена регрессионного уравнения;

д) Multiple R: коэффициент множественной корреляции;

е) R: коэффициент детерминации. Это очень важный показатель в регрессионном анализе. Он изменяется от 0 до 1 и отражает «качество» рассчитанной регрессии, показывая долю (%) общего разброса выборочных точек, которая «объясняется» построенной регрессией (например, при R² = 0,85, следует вывод о том, что 85% дисперсии зависимой переменной y объясняется вариацией независимой переменной х);

ж) Adjusted R²: скорректированный на число степеней свободы коэффициент детерминации (Adjusted R-square = 1 - (1 - R-square)x[n/(n - p)], где n - число наблюдений, р - число независимых переменных плюс 1);

з) Standard error of estimate: параметр, отражающий степень разброса выборочных значений относительно линии регрессии;

и) F, dfиp: F-критерий, число степеней свободы, принятое при его расчете, и вероятность ошибки для нулевой гипотезы F-теста. F-тест в регрессионном анализе применяется для оценки статистической значимости модели. При p<0,05 можно заключить, что рассчитанная регрессия удовлетворительно описывает связь между исследуемыми признаками;

к) t(df) и p: критерий Стьюдента t используется для проверки нулевой гипотезы о равенстве 0 свободного члена регрессионного уравнения. Р - вероятность ошибки для этой нулевой гипотезы;

л) beta: стандартизованный коэффициент регрессии - это коэффициент регрессии, который мы получили бы в случае предварительной стандартизации обеих переменных (т.е. при таком преобразовании, когда их средние значения стали бы равны 0, а стандартные отклонения - 1). Расчет beta позволяет оценить, в какой степени значения зависимой переменной определяются значениями независимой переменной. Beta может оказаться особенно полезным показателем при включении в анализ нескольких независимых переменных, выражающихся в разных единицах измерения - в таком случае коэффициент отражал бы удельный вклад каждой из этих переменных в вариацию зависимой переменной. При наличии одной независимой переменной коэффициент beta идентичен Multiple R.

Нажмите кнопку «Summary: Regression results»(Результаты регрессионного анализа). Появится таблица с результатами анализа, в которой:

а) Beta: стандартизованный коэффициент регрессии;

б) Std. err. of beta: стандартная ошибка стандартизованного коэффициента регрессии;

в) В: один из самых важных столбцов в этой таблице, поскольку именно он содержит искомые значения свободного члена регрессионного уравнения (в строке Intercept) и коэффициента регрессии (нижняя строка таблицы);

г) Std. err. of B: стандартные ошибки коэффициентов уравнения;

д) t(df): значения t-критерия Стьюдента, который используется для проверки гипотезы о равенстве обоих коэффициентов уравнения 0;

е) p-level: вероятность ошибки для нулевой гипотезы о равенстве коэффициентов уравнения нулю.

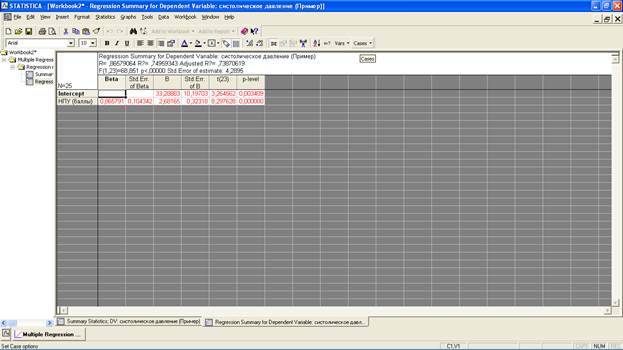
Из итоговой таблица видно, что оба коэффициента регрессии статистически значимо отличаются от 0 (p < 0,05) и что в целом построенная регрессионная модель отлично описывает связь между систолическим давлением и нервно-психической устойчивостью. Само же рассчитанное уравнение мы можем записать следующим образом:

Н= 2,682 x А + 33,289, где Н - давление, А – нервно-психическая устойчивость человека.

Важной частью регрессионного анализа является анализ остатков (остатки представляют собой разности между наблюдаемыми значениями зависимой переменной и теми ее значениями, которые предсказываются регрессионной моделью). Он запускается путем нажатия кнопки «Perform residual analysis» (Выполнить анализ остатков) на закладке «Residuals /Assumptions /Predictions» (Остатки / Условия / Предсказания).

Первое, что нужно проверить в отношении остатков - это нормальностьих распределения. Для этого на закладке «Quick»подмодуля анализа остатков нажмите кнопку «Normal plot of residuals», чтобы построить график нормальных вероятностей. Если точки на этом графике достаточно тесно укладываются вдоль теоретически ожидаемой прямой, то можно заключить, что остатки распределяются нормально. Иначе линейная регрессионная модель для анализируемых переменных будет неприменима.

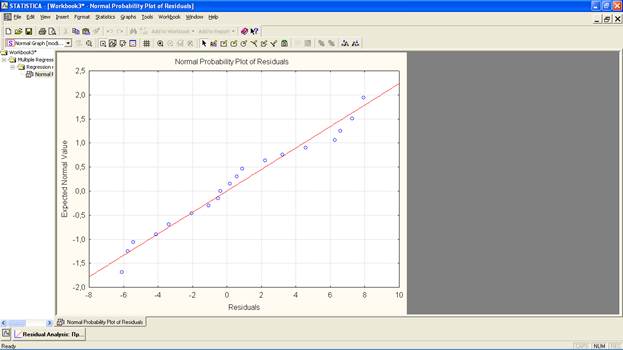
Второе условие в отношении остатков состоит в том, что их дисперсия должна оставаться неизменной во всем диапазоне значений анализируемых переменных. Для проверки этого условия на закладке «Scatterplots» (Диаграммы рассеяния) нажмите кнопку «Predicted vs. Residuals», чтобы построить график зависимости значений остатков от предсказываемых моделью значений зависимой переменной. Если проверяемое условие выполняется, то точки на этом графике будут располагаться хаотично, не проявляя никакой закономерности. Если же в расположении точек имеется тенденция (разброс увеличивается слева направо, точки тесно укладываются вдоль прямой, и т.п.), линейный регрессионный анализ также неприменим.

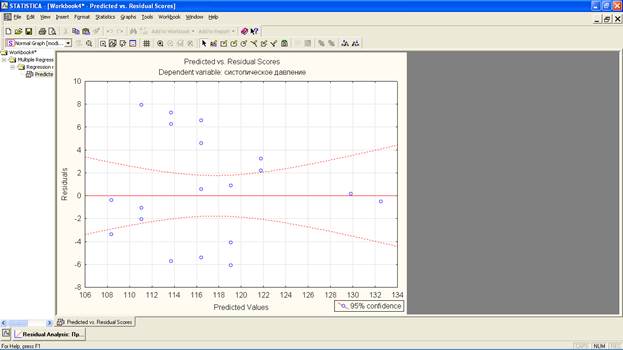
В рассмотренном примере оба условия в отношении остатков выполняются, что еще раз подтверждает адекватность рассчитанной регрессионной модели для описания связи между артериальным давлением и нервно-психической устойчивостью.

ЛИТЕРАТУРА

1) Дружинин В.Н. Экспериментальная психология. - СПб.: Питер, 2011.

2) Ермолаев О.Ю. Математическая статистика для психологов: Учебник. - М.: МПСИ, Флинта, 2011.

3) Корнилова Т.В. Экспериментальная психология: Теория и методы. - М.: Юрайт-Издат, 2012.

4) Куликов Л.В. Психологическое исследование: методические рекомендации по проведению. – СПб.: Речь, 2001. - с.90-92.

5) Практикум по общей, экспериментальной и прикладной психологии /Под ред. А.А.Крылова, С.А.Маничева. - СПб.: Питер, 2007.

6) Сидоренко Е.В. Методы математической обработки в психологии. – СПб.: ООО «Речь», 2000. – 350 с.

7) Худяков А. И. Экспериментальная психология в схемах и комментариях. – СПб.: Питер, 2008.

Приложение 1

Таблица 1

Значения критерия t_st для отбраковки выпадающих вариант

при разных уровнях значимости (p).

	p		p
n	0,05	0,01	0,001	n	0,05	0,01	0,001
-	-	-	-	-	-	-	-
	3,04	5,04	9,43		2,145	2,932	3,979
	2,78	4,36	7,41		2,105	2,852	3,819
	2,62	3,96	6,37		2,079	2,802	3,719
	2,51	3,71	5,73		2,061	2,768	3,652
	2,43	3,54	5,31		2,048	2,742	3,602
	2,37	3,41	5,01		2,038	2,722	3,565
	2,33	3,31	4,79		2,030	2,707	3,532
	2,29	3,23	4,62		2,018	2,683	3,492
	2,26	3,17	4,48		2,009	2,667	3,462
	2,24	3,12	4,37		2,003	2,655	3,439
	2,22	3,08	4,28		1,998	2,646	3,423
	2,20	3,04	4,20		1,994	2,639	3,409
	2,18	3,01	4,13	∞	1,960	2,576	3,291
	2,17	2,98	4,07

Таблица 2

Значение функции f(o_i)

(ординаты нормальной кривой)

o_i	Сотые доли o_i

0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
4,0

Примечание. Значения вероятности p даны числами после запятой.

Таблица 3

Критические значения критерия c² для уровней статистической значимости р£0,05 и р£0,01 при разном числе степеней свободы V.

Различия между двумя распределениями могут считаться достоверными, если c²_эмп достигает или превышает c²_0,05, и тем более достоверными, если c²_эмп достигает или превышает c²_0,01 (по Большеву Л.Н., Смирнову Н.В., 1983).

р	p	р
V	0,05	0,01	V	0,05	0,01	V	0,05	0,01
	3,841	6,635		49,802	57,342		89,391	99,227
	5,991	9,210		50,998	58,619		90,631	100.425
	7,815	11,345		52,192	59,892		91,670	101,621
	9,488	13,277		53,384	61,162		92,808	102,816
	11,070	15,086		54,572	62,428		93,945	104,010
	12,592	16,812		55,758	63,691		95,081	105,202
	14.067	18.475		56.942	64,950		96,217	106,393
	15,507	20,090		58,124	66,206		97,351	107,582
	16,919	21,666		59,304	67,459		98.484	108,771
	18,307	23,209		60,481	68.709		99.617	109,958
	19,675	24,725		61,656	69,957		100,749	111,144
	21,026	26,217		62,830	71,201		101.879	112,329
	22,362	27,688		64,001	72,443		103,010	113,512
	23.685	29,141		65,171	73,683		104,139	114,695
	24,996	30,578		66,339	74,919		105,267	115.876
	26,296	32,000		67,505	76,154		106,395	117,057
	27,587	33,409		68,669	77,386		107,522	118,236
	28,869	34,805		69,832	78,616		108,648	119,414
	30,144	36,191		70,993	79.84'3		109,773	120,591
	31,410	37,566		72.153	81,069		110,898	121,767
	32,671	38,932		73,311	82,292		112,022	122,942
	33,924	40,289		74,468	83,513		113,145	124,116
	35,172	41,638		75,624	84,733		114,268	125,289
	36,415	42,980		76,778	85.950		115,390	126,462
	37,652	44,314		77,931	87,166		116,511	127,633
	38,885	45,642		79,082	88.379		117,632	128.803
	40.113	46,963		80,232	89,591		118,752	129,973
	41,337	48,278		81,381	90,802		119,871	131,141
	42,557	49.588		82,529	92.010		120,990	132,309
	43,773	50,892		83,675	93,217		122,108	133,476
	44,985	52,191		84,821	94,422		123,225	134,642
	46,194	53,486		85,965	95,626		124,342	135,807
	47.400	54,776		87,108	96,828
	48.602	56,061		88,250	98,028

Таблица 4

Значения критерия t Стьюдента при различных уровнях значимости (р)

Число степеней свободы d	Уровень значимости
0,05	0,01	0,001
	12,71	63,66	-
	4,30	9,93	31,60
	3,18	5,84	12,94
	2,78	4,60	8,61
	2,57	4,03	6,86
	2,45	3,71	5,96
	2,37	3,50	5,41
	2,31	3,36	5,04
	2,26	3,25	4,78
	2,23	3,17	4,59
	2,20	3,11	4,44
	2,18	3,06	4,32
	2,16	3,01	4,22
	2,15	2,98	4,14
	2,13	2,95	4,07
	2,12	2,92	4,02
	2,11	2,90	3,97
	2,10	2,88	3,92
	2,09	2,86	3,88
	2,09	2,85	3,85
	2,08	2,83	3,82
	2,07	2,82	3,79
	2,07	2,81	3,77
	2,06	2,80	3,75
	2,06	2,79	3,73
	2,06	2,78	3,71
	2,05	2,77	3,69
	2,05	2,76	3,67
	2,05	2,76	3,66
	2,04	2,75	3,65
	1,96	2,58	3,29

Приложение 2

Таблица 1

Критические значения выборочного коэффициента корреляции рангов R_s Спирмена

z	р	z	р	z	р
0,05	0,01	0,05	0,01	0,05	0,01
	0,94			0,48	0,62	0,37	0,48
	0,85			0,47	0,60	0,36	0,47
	0,78	0,94		0,46	0,58	0,36	0,46
	0,72	0,88		0,45	0,57	0,36	0,45
	0,68	0,83		0,44	0,56	0,34	0,45
	0,62	0,79		0,43	0,54	0,34	0,44
	0,61	0,76		0,42	0,53	0,33	0,43
	0,58	0,73		0,41	0,52	0,33	0,43
	0,56	0,70		0,40	0,51	0,33	0,42
	0,54	0,68		0,39	0,50	0,32	0,41
	0,52	0,66		0,38	0,49	0,32	0,41
	0,50	0,64		0,38	0,48	0,31	0,40
П р и м е ч а н и е – Здесь p – уровень значимости, z – объем выборки. Если вычисленное значение R_s<R_s_0,05, то корреляция не является статистически значимой. Если эмпирическое значение R_s≥R_s_0,01, то корреляция является достоверной.

Таблица 2

Критические значения коэффициента корреляции r_xy Пирсона

n\P	0,05	0,01	n\P	0,05	0,01
	0,950	0,990		0,388	0,496
	0,878	0,959		0,381	0,487
	0,811	0,917		0,371	0,478
	0,754	0,874		0,367	0,470
	0,707	0,834		0,361	0,463
	0,666	0,798		0,332	0,435
	0,632	0,765		0,310	0,407
	0,602	0,735		0,292	0,384
	0,576	0,708		0,277	0,364
	0,553	0,684		0,253	0,333
	0,532	0,661		0,234	0,308
	0,514	0,641		0,219	0,288
	0,497	0,623		0,206	0,272
	0,482	0,606		0,196	0,258
	0,468	0,590		0,175	0,230
	0,456	0,575		0,160	0,210
	0,444	0,561		0,138	0,182
	0,433	0,549		0,142	0,163
	0,423	0,537		0,113	0,148
	0,413	0,526		0,098	0,128
	0,404	0,515		0,088	0,115
	0,396	0,505		0,062	0,081

Примечания: корреляция статистически значима, если r_xy≥ r_xy_0,01. Если

r_xy<r_xy_0,05, то корреляция не является значимой.

Приложение 3

<2 3 4 567 8 >

Дата добавления: 2016-03-10; просмотров: 1656;