Корреляционный анализ. В практике экспериментальных исследований нередки случаи, когда предполагается наличие связанных изменений каких-либо двух статистических признаков
В практике экспериментальных исследований нередки случаи, когда предполагается наличие связанных изменений каких-либо двух статистических признаков. Например, представляются взаимозависимыми вариации величины роста и веса тела людей (прямая связь), силы мышц и их подвижности (обратная связь) и т.д. Такого рода связи и закономерности не являются строго однозначными или функциональными; они, так же как и сами вариации признаков, являются статистическими, или корреляционными.
Теория корреляционного исследования, основанная на представлениях о мерах корреляционной связи, разработана К. Пирсоном.
Корреляционным называется исследование, проводимое для подтверждения или опровержения гипотезы о статистической связи между несколькими (двумя и более) переменными. В психологии в качестве переменных могут выступать психические свойства, процессы, состояния и др [2].
Корреляция - это связь между статистическими вариациями (выборками) по различным признакам, между влияниями каких-либо двух факторов, формирующих данное статистическое распределение.
«Корреляция» в прямом переводе означает «соотношение». Если изменение одной переменной сопровождается изменением другой, то можно говорить о корреляции этих переменных. Наличие корреляции двух переменных ничего не говорит о причинно-следственных зависимостях между ними, но дает возможность выдвинуть такую гипотезу. Отсутствие же корреляции позволяет отвергнуть гипотезу о причинно-следственной связи переменных [3].
Коэффициент корреляции - это математический показатель силы (тесноты) связи между двумя сопоставляемыми статистическими признаками.
По какой бы формуле ни вычислялся коэффициент корреляции, его величина колеблется в пределах от -1 до +1. Смысл крайних значений коэффициента состоит в следующем:
n если коэффициент корреляции равен 1, значит, связь между признаками однозначна (функциональная, нестатистическая), по типу прямо пропорциональной зависимости;
n если коэффициент равен - 1, то связь также является функциональной, но по типу обратной пропорциональности;
n нулевая величина коэффициента корреляции говорит о полном отсутствии связи (по типу линейной) между сопоставляемыми признаками.
Психологам часто хочется получать ответы на такие вопросы, эмпирические данные для которых могут быть собраны только в корреляционном исследовании. Проверка соответствующих гипотез, если они понимаются именно как гипотезы о взаимосвязях переменных, а не о причинной зависимости, может вести к обоснованным выводам.
Всякое вычисленное (эмпирическое) значение коэффициента корреляции должно быть проверено на статистическую значимость (таблицы 1 или 2 приложения 3).
Если эмпирическое значение коэффициента корреляции меньше или равно табличному для р = 0,05, то корреляция является незначимой. Если вычисленное значение коэффициента корреляции больше табличного для р = 0,01, корреляция статистически значима (существенна, реальна). В случае, когда величина коэффициента заключена между двумя табличными, на практике говорят о значимости корреляции для р = 0,05. Однако строго вероятностная трактовка этого факта несколько иная: мы не можем утверждать отсутствия корреляции, но ее статистически доказанного наличия также еще нет.
Простейшей формой коэффициента корреляции является коэффициент ранговой корреляции Rs (коэффициент Спирмена), который измеряет связь между рангами (местами) данной варианты по разным признакам, но не между собственными величинами варианты. Здесь исследуется связь качественная, чем строго количественная, хотя ранг сам по себе - это уже и количественный признак.
Rs = 1- 6*Sd2/(n3 – n), (4.1)
где n - объем совокупности, длина одного статистического ряда;
d - разность между рангами каждой варианты по двум коррелируемым признакам.
Пример вычисления. Десять испытуемых (А, Б, В и т.д.) расположились в порядке увеличения возраста и пространственного порога в следующих последовательностях (таблица 4.1):
Таблица 4.1
| Испытуемые | Ранг по возрасту | Ранг по пространств. порогу | d | d2 |
| А | -5 | |||
| Б | -3 | |||
| В | ||||
| Г | ||||
| Д | -5 | |||
| Е | ||||
| Ж | -2 | |||
| З | ||||
| И | ||||
| К |
n = 10 Sd2 = 128
Rs = 1 - 6*128/(1000 – 10) = 1 - 768/990 = 0,22
Rs = 0,22.
Так как по данным таблицы 1 (приложение 2) Rs0,05 = 0,64, и эмпирическое значение Rs<Rs0,05, корреляция между местами испытуемых по величине порогов и по возрасту не является статистически значимой.
Пример применения в психологических исследованиях коэффициента корреляции Rs Спирмена приведен в приложении 3 настоящего учебного пособия (пример 1).
Используемый в исследованиях коэффициент корреляции рангов, предложенный К. Спирменом, относится к непараметрическим показателям связи между переменными, измеренными в ранговой шкале. При расчете этого коэффициента не требуется никаких предположений о характере распределений признаков в генеральной совокупности. Данный коэффициент определяет степень тесноты связи порядковых признаков, которые в этом случае представляют собой ранги сравниваемых величин [8].
Величина коэффициента линейной корреляции Спирмена лежит в интервале +1 и -1. Он может быть положительным и отрицательным, характеризуя направленность связи между двумя признаками, измеренными в ранговой шкале.
Для применения коэффициента корреляции Спирмена (r), необходимо соблюдать следующие условия [2]:
1. Сравниваемые переменные должны быть получены в порядковой (ранговой) шкале, но могут быть измерены также в шкале интервалов и шкале отношений.
2. Число варьирующих признаков в сравниваемых переменных X и У должно быть одинаковым.
Пример задачи: Исследователь должен выяснить, как связаны между собой значения пяти шкал методики изучения самооценки (Дембо-Рубинштейн): «ум», «характер», «красота», «здоровье», «счастье».
Решение: После проведения подготовительных работ с документом (см. Приложение 4) он будет выглядеть следующим образом:
Выберите «Statistics» («Статистика») > «Nonparametrics» («Непараметрические…») > «Correlations…» («Корреляция…») и нажмите на «OK»:
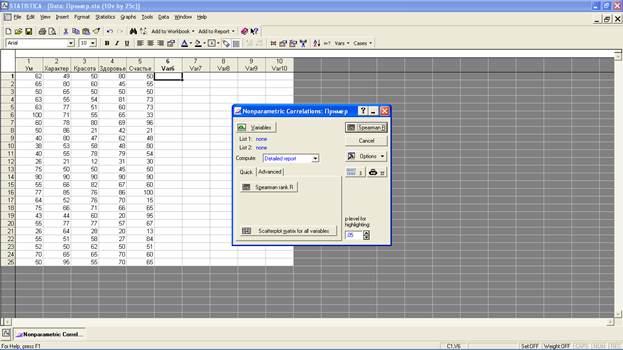
В открывшемся диалоговом окне («Nonparametric Correlations») в строчке «Compute» (с анг. яз., «расчет») по умолчанию стоит «Detailed report» (с анг. яз., «детализированный отчет»). Вы можете по своему усмотрению выбрать другие режимы расчета. Нажмите кнопку «Variables» и выберите колонки с требуемыми переменными, после чего нажмите «ОК»:
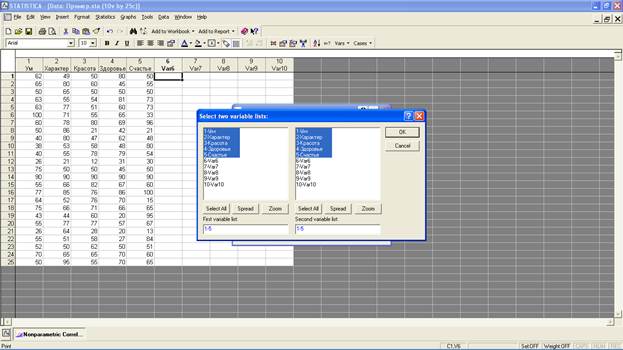
Далее нажмите на кнопку «Spearman R»:
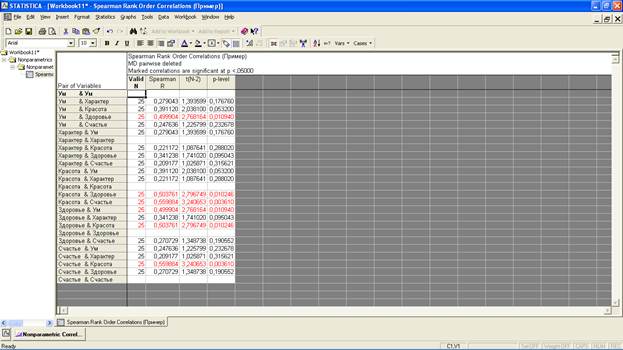
В появившейся таблице в крайней левой колонке представлены коррелируемые переменные, в колонке (Valid N) – количество участвующих в исследовании испытуемых, в колонке (Spearman R) – значение коэффициента корреляции r-Спирмена, в колонке (t(N-2)) – площадь пересечения распределений Стьюдента у коррелируемых переменных, в последней колонке (p-level) указан уровень значимости.
В нашем примере мы выявили три пары переменных, между которыми образуются корреляционная связь: «Ум & Здоровье», «Красота & Здоровье», «Красота & Счастье».
Другой очень распространенной формой коэффициента линейной корреляции является коэффициент корреляции Пирсона rxy:
rxy = X*Y/X2*Y2, (4.2)
где Х = xi – Xсp, Y = yi – Yсp.
Эта формула сопоставляет сами величины признаков и, в конечном счете, основана на вычислении “совместной дисперсии” s2 xy двух переменных xi и yi и на делении ее на произведение отдельных среднеквадратических отклонений, т.е.
rxy = s2xy/sx*sy. (4.3)
Пример вычисления. Десять испытуемых (А, Б, В, и т.д.) в эксперименте по заучиванию двузначных чисел дали по первой пробе такие результаты: 3, 4, 4, 5, 3, 4, 5, 2, 3, 5 (xi). Эти же испытуемые при непроизвольном запоминании слов имели такие показатели: 5, 9, 8, 6, 4, 5, 8, 7, 5, 6 (yi). Посмотрим, коррелируют ли между собой два этих показателя эффективности запоминания.
Вычисления удобнее вести в специальной таблице 4.2.
Таблица 4.2
| Испыту-емые | (xi) | (yi) | X = xi-Xсp | Y = yi-Yсp | XY | X2 | Y2 |
| A | -0,8 | -1,3 | 1,04 | 0,64 | 1,69 | ||
| Б | 0,2 | 2,7 | 0,54 | 0,04 | 7,29 | ||
| В | 0,2 | 1,7 | 0,34 | 0,04 | 2,89 | ||
| Г | 1,2 | -0,3 | -0,36 | 1,44 | 0,09 | ||
| Д | -0,8 | -2,3 | 1,84 | 0,64 | 5,29 | ||
| Е | 0,2 | -1,3 | -0,26 | 0,04 | 1,69 | ||
| Ж | 1,2 | 1,7 | 2,04 | 1,44 | 2,89 | ||
| З | -1,8 | 0,7 | -1,26 | 3,24 | 0,49 | ||
| И | -0,8 | -1,3 | 1,04 | 0,64 | 1,69 | ||
| К | 1,2 | -0,3 | -0,36 | 1,44 | 0,09 | ||
| S | 4,6 | 9,6 | 24,1 |
Хср = 38/10 = 3,8 Уср = 63/10 = 6,3.
rxy = Х*Y/Х2*Y2 = 4,6/9,6*24,1 = 4,6/231,36 = 0,2.
По данным таблицы 2 (приложение 2), rxy0,05(10) = 0,632, поэтому корреляция между двумя показателями эффективности памяти данной группы испытуемых не является статистически значимой.
Дата добавления: 2016-03-10; просмотров: 1699;
