Статистические критерии различия
3.1. Выбор статистического критерия различия
Одной из наиболее часто встречающихся статистических задач, с которыми сталкивается психолог, является задача сравнения результатов обследования какого-либо психологического признака в разных условиях измерения (например, до и после определенного воздействия) или обследования контрольной и экспериментальной групп. Помимо этого нередко возникает необходимость оценить характер изменения того или иного психологического показателя в одной или нескольких группах в разные периоды времени или выявить динамику изменения этого показателя под влиянием экспериментальных воздействий.
Для решения подобных задач используется достаточно большой набор статистических способов, называемых в наиболее общем виде критериями различий. Эти критерия позволяют оценить степень статистической достоверности различий между разнообразными показателями, измеренными согласно плану проведения психологического исследования.
Существует достаточно большое количество критериев различий. Каждый из них имеет свою специфику, различаясь между собой по различным основаниям. Одним из таких оснований является тип измерительной шкалы, для которой предназначен тот или иной критерий. Например, с помощью некоторых критериев можно обрабатывать данные, полученные только в номинальных шкалах. Ряд критериев дает возможность обрабатывать данные, полученные в порядковой, интервальной и шкале отношений.
Критерии различаются также по максимальному объему выборки, который они могут охватить, а также и по количеству выборок, которые можно сравнивать между собой с их помощью. Так, существуют критерии, позволяющие оценить различия сразу в трех и большем числе выборок. Некоторые критерии позволяют сопоставлять неравные по численности выборки.
Еще одним признаком, дифференцирующим критерии, служит само качество выборки: она может быть связной (зависимой) или несвязной (независимой). Выборки также могут быть взяты из одной или нескольких генеральных совокупностей. Именно эта характеристика выборки служит наиболее важным основанием, по которому, прежде всего, выбираются критерии.
Кроме того, критерии различаются по мощности. Психолог может решать экспериментальные задачи с использованием разных статистических критериев. При этом возможна такая ситуация, что один критерий позволяет обнаружить различия, а другой критерий различий не выявляет. Последнее означает, что первый критерий оказывается более мощным, чем другой.
Все критерии различий условно подразделены на две группы: параметрические и непараметрические критерии.
Критерий различия называют параметрическим, если он основан на конкретном типе распределения генеральной совокупности (как правило, нормальном) или использует параметры этой совокупности (средние, дисперсии и т.д.). Критерий различия называют непараметрическим, если он не базируется на предположении о типе распределения генеральной совокупности и не использует параметры этой совокупности [2].
При нормальном распределении генеральной совокупности параметрические критерии обладают большей мощностью по сравнению с непараметрическими. Иными словами, они способны с большей достоверностью отвергать нулевую гипотезу, если последняя неверна. По этой причине в тех случаях, когда выборки взяты из нормально распределенных генеральных совокупностей, следует отдавать предпочтение параметрическим критериям. Однако, как показывает практика, подавляющее большинство данных, получаемых в психологических экспериментах, не распределены нормально [2]. Поэтому применение параметрических критериев при анализе результатов психологических исследований может привести к ошибкам в статистических выводах. В таких случаях непараметрические критерии оказываются более мощными, т.е. способными с большей достоверностью отвергать нулевую гипотезу.
Анализ частотных распределений эмпирических данных, полученных в ходе психодиагностических обследований испытуемых, необходим для выбора способов их математико-статистической обработки. От результатов такой оценки во многом зависит, например, выбор критериев выявления различий в психологических характеристиках, полученных в различных группах испытуемых, или сдвига исследуемой психологической характеристики в ходе экспериментального воздействия или формирующего эксперимента.
Для правильной статистической обработки результатов психологических исследований должны соблюдаться правила по выбору параметрических и непараметрических критериев, позволяющих выявлять различия в исследуемых психологических характеристиках.
Для психологических характеристик, имеющих нормальное распределение или близкое к нормальному, необходимо использовать параметрические критерии, которые являются более мощными, чем непараметрические критерии. Достоинством непараметрических критериев является то, что они позволяют проверять статистические гипотезы независимо от формы распределения.
В подразделе 2.1 представлен способ оценки нормальности распределения выборочных данных на основе первичных статистик.
В данном разделе приводится пример более точной и строгой оценки нормальности распределения с помощью критерия «хи-квадрат» Пирсона χ2эмп.
Критерий «хи-квадрат» в одном из вариантов своего использования применяется при расчете согласия эмпирического и предполагаемого теоретического распределения – в этом случае проверяется гипотеза Н0 об отсутствии различий между теоретическим и эмпирическим распределениями [2].
Рассмотрим задачу, в которой в качестве теоретического будет использоваться нормальное распределение (Задача взята из учебника О.Ю. Ермолаева «Математическая статистика для психологов», 2002) [2].
Задача.У 267 человек был измерен рост. Вопрос состоит в том, будет ли полученное в этой выборке распределение роста близко к нормальному?
Решение. Измерения проводились с точностью до 0,1 см и все полученные величины роста оказались в диапазоне от 156,5 до 183,5. Для расчета по критерию «хи-квадрат» целесообразно разбить этот диапазон на интервалы, например, по 3 см каждый. Тогда все экспериментальные данные будут распределены по 9 интервалам: (183,5-156,5)/3=9. При этом центрами интервалов будут следующие числа: 158, 161, 164 и т.д. до 182.
При измерении роста в каждый из этих интервалов попало какое-то количество людей – эта величина для каждого интервала и будет эмпирической частотой, обозначаемой в дальнейшем как fэi.
Чтобы применить расчетную формулу для вычисления значения критерия «хи-квадрат»:
k
χ2эмп=Σ∆i2/fmi , (3.1)
i=1
где ∆i - разность между эмпирическими и «теоретическими» частотами;
k – количество разрядов признака;
fmi - вычисленная, или «теоретическая» частота;
необходимо, прежде всего, вычислить теоретические частоты. Для этого по всем выборочным данным нужно вычислить среднее М и стандартное отклонение sпо известным из литературных источников формулам [5].В качестве тренировки слушателям предлагается проверить себя и самостоятельно рассчитать обозначенные параметры распределения выборочных данных двумя способами: вручную и с помощью программ статистической обработки данных; сравнить полученные двумя способами значения одноименных параметров между собой, а также со значениями, указанными в данном учебном пособии.
Для наших выборочных данных величина Моказалась равной 166,22 и величина s получилась равной 4,06.
Затем для каждого выделенного интервала следует подсчитать величины oi (индекс I меняется от 1 до 9) по формуле:
oi = (хi-М)/s. (3.2)
Величины oi называются нормированными частотами. Удобнее производить их расчет в приведенной ниже таблице 3.1:
Таблица 3.1
| №1 | №2 | №3 | №4 | №5 |
| Центры интервалов xi | Эмпирические частоты fэi | Нормированные частоты oi | Ординаты нормальной кривой f(oi) | Расчетные теоретические частоты fтi |
| -2,77 | 0,0086 | 1,6 | ||
| -2,03 | 0,0508 | 10,0 | ||
| -1,29 | 0,1736 | 34,3 | ||
| -0,55 | 0,3429 | 67,8 | ||
| +0,19 | 0,3918 | 77,6 | ||
| +0,93 | 0,2589 | 51,2 | ||
| +1,67 | 0,0989 | 19,5 | ||
| +2,41 | 0,0219 | 4,4 | ||
| +3,15 | 0,0028 | 0,6 | ||
| S | - | - |
Затем для каждой oi по таблице 2 (приложение 1) находят величины f(oi), которые называются ординаты нормальной кривой.
Расчет теоретических частот осуществляется для каждого интервала по следующей формуле:
fтi = f(oi)*(n*λ)/s, (3.3)
где n=267 – общая величина выборки;
λ=3 – величина интервала;
s - стандартное отклонение.
Все рассчитанные значения заносятся в соответствующие столбцы таблицы 3.1.
После заполнения таблицы 3.1 все готово для работы с критерием «хи-квадрат» на основе стандартной таблицы. В целях упрощения расчетов сократим число интервалов до 7 за счет сложения двух верхних и двух нижних частот. Тогда стандартная таблица для вычисления «хи-квадрат» будет выглядеть так:
Таблица 3.2
| №1 | №2 | №3 | №4 | №5 | №6 |
| Номера интервалов (альтернативы) | fэi | fтi | (fэi- fтi) | (fэi- fтi)2 | (fэi- fтi)2/fтi |
| 11,6 | +0,4 | 0,16 | 0,01 | ||
| 34,3 | -3,3 | 10,89 | 0,32 | ||
| 67,8 | +3,2 | 10,24 | 0,15 | ||
| 77,6 | +4,4 | 19,36 | 0,25 | ||
| 51,2 | -5,2 | 27,04 | 0,53 | ||
| 19,5 | -0,5 | 0,25 | 0,01 | ||
| 5,0 | +1,0 | 1,00 | 0,20 | ||
| S | χ2эмп=1,47 |
В случае оценки равенства эмпирического распределения нормальному число степеней свободы определяется особым образом: из общего числа интервалов вычитается число 3. Таким образом, число степеней свободы в нашем примере будет равно ν=4.
По таблице 3 (приложение 1) находим критические значения критерия «хи-квадрат»:
χ2кр.1=9,488 (для р≤0,05),
χ2кр.2=13,277 (для р≤0,01).
Строим «ось значимости»:

Полученная величина эмпирического значения «хи-квадрат» попала в зону незначимости, поэтому необходимо принять гипотезу Н0 об отсутствии различий. Следовательно, существуют все основания утверждать, что наше эмпирическое распределение близко к нормальному.
Несмотря на некоторую «громоздкость» вычислительных процедур, этот способ расчета дает наиболее точную оценку совпадения эмпирического и нормального распределений.
Пример применения в психологических исследованиях критерия «хи-квадрат» приведен в приложении 3 настоящего учебного пособия (пример 2).
Домашнее задание. В качестве домашнего задания для тех слушателей, которые хорошо владеют навыками статистической обработки данных с помощью компьютерных программ, предлагается рассчитать критерий «хи-квадрат» на одном из известных и популярных статистических пакетов и сравнить с результатом решения задачи, полученным вручную, как описано в настоящем учебном пособии.
Возвращаясь к разобранной задаче, не лишним будет обозначить критерии выявления различий, которыми целесообразно пользоваться при обработке эмпирических данных. При принятии гипотезы Н0 для обработки данных выбирают t-критерий Стьюдента или F-критерий Фишера. При опровержении гипотезы Н0 выбирают критерий знаков G, парный критерий Т-Вилкоксона, критерий Фридмана, критерий тенденций Пейджа, критерий Макнамары, которые рассматриваются для условий связанных выборок, или критерий U Вилкоксона-Манна-Уитни, критерий Q Розенбаума, H-критерий Крускала-Уоллиса, S-критерий тенденций Джонкира, которые рассматриваются для условий несвязанных выборок. Все эти критерии подробно, с примерами рассматриваются у О.Ю. Ермолаева, Е.В. Сидоренко [2,6].
Одной из наиболее часто встречающихся задач при обработке данных является оценка достоверности отличий между двумя или более рядами значений [4]. В математической статистике существует ряд способов для этого. Для использования большинства мощных критериев требуются дополнительные вычисления, обычно весьма развернутые.
Во многих прикладных статистических программах есть процедуры оценки различий между параметрами одной выборки или разных выборок. При полностью компьютеризованной обработке материала нетрудно в нужный момент использовать соответствующую процедуру и оценить интересующие различия. Однако, большинство психологов не имеют свободного и неограниченного доступа для работы с компьютером - либо недостаточен парк ЭВМ, либо психолог как пользователь ЭВМ неподготовлен и может проводить обработку только с помощью квалифицированного персонала. И в том, и в другом случае типичный сеанс работы с компьютером заканчивается тем, что психолог получает принтерные распечатки, содержащие подсчитанные первичные статистики, результаты корреляционного анализа, иногда и факторного (компонентного).
Основной анализ осуществляется позже, не в диалоге с ЭВМ. Исходя из этих рассуждений, будем считать, что перед психологом часто встает задача оценки достоверности различий, используя ранее вычисленные статистики. При сравнении средних значений признака говорят о достоверности (недостоверности) отличий средних арифметических, а при сравнении изменчивости показателей - о достоверности (недостоверности) отклонений сигм (дисперсий) и коэффициентов вариации.
Достоверность различий средних арифметических можно оценить по достаточно эффективному параметрическому критерию Стьюдента. Он вычисляется по формуле:
M1 - M2
t = ----------------, (3.4)
(m12 +m22)1/2
где M1 и M2 - значения сравниваемых средних арифметических,
m1 и m2 - соответствующие величины статистических ошибок средних арифметических (вычисляются по формуле (1.6)).
Значения критерия Стьюдента t для трех уровней значимости (p) приведены в таблице 4 (приложение 1). Число степеней свободы определяется по формуле:
d = n1+ n2 - 2, (3.5)
где n1 и n2 - объемы сравниваемых выборок.
С уменьшением объемов выборок (n<10) критерий Стьюдента становится чувствительным к форме распределения исследуемого признака в генеральной совокупности. Поэтому в сомнительных случаях рекомендуется использовать непараметрические методы или сравнивать полученные значения с критическими (приведенными в таблице) для более высокого уровня значимости.
Решение о достоверности различий принимается в том случае, если вычисленная величина t превышает табличное значение для данного числа степеней свободы. В тексте публикации или научного отчета указывают наиболее высокий уровень значимости из трех: 0,05, 0,01 или 0,001.
Если превышены 0.05 и 0.01, то пишут (обычно в скобках) р = 0,01 или p < 0,01. Это означает, что оцениваемые различия все же случайны только с вероятностью не более 1 из 100 шансов. Если превышены табличные значения для всех трех уровней: 0,05, 0,01 и 0,001, то указывают р = 0,001 или p < 0,001, что означает случайность выявленных различий между средними не более 1 из 1000 шансов.
Пример оценкидостоверности различий средних арифметических по критерию Стьюдента:
М1= 113,3, m1= 2,4, n1= 13 ; M2= 103,3, m2 = 2,6, n2= 16.
113,3-103,3
t = ----------------------- = 2,83.
(2,42 + 2,62)1/2
Для числа степеней свободы d = 13 + 16 - 2 = 27 вычисленная величина превышает табличную 2,77 для вероятности р = 0,01. Следовательно, различия между средними достоверны на уровне 0,01.
Приведенная формула проста. Используя ее, можно с помощью простейшего бытового калькулятора с памятью вычислить t критерий без промежуточных записей.
Следует помнить, что при любом численном значении критерия достоверности различия между средними этот показатель оценивает не степень выявленного различия (она оценивается по самой разности между средними), а лишь статистическую достоверность его, т.е. право распространять полученный на основе сопоставления выборок вывод о наличии разницы на все явление (весь процесс) в целом. Низкий вычисленный критерий различия не может служить доказательством отсутствия различия между двумя признаками (явлениями), ибо его значимость (степень вероятности) зависит не только от величины средних, но и от численности сравниваемых выборок. Он говорит не об отсутствии различия, а о том, что при данной величине выборок оно статистически недостоверно: слишком велик шанс, что разница при данных условиях определения случайна, слишком мала вероятность ее достоверности.
Степень, т.е. величину выявленного различия, желательно оценивать, опираясь на содержательные критерии. Вместе с тем, для психологического исследования весьма характерно наличие множества показателей, которые, по существу, являются условными баллами, и валидность оценивания с помощью них еще предстоит доказать. Чтобы избежать большей произвольности, в таких случаях также приходится опираться на статистические параметры.
Пожалуй, наиболее распространено для этого использование сигмы. Разницу между двумя значениями в одну сигму и более можно считать достаточно выраженной. Если сигма подсчитана для ряда значений более 35, то достаточно выраженной можно рассматривать и разницу в 0,5 сигмы. Однако, для ответственных выводов о том, насколько велика разница между значениями, лучше использовать строгие критерии.
При оценке различий в распределениях, далеких от нормального, непараметрические критерии могут выявить значимые различия, в то время как параметрические критерии таких различий не обнаружат. Важно отметить, что непараметрические критерии выявляют значимые различия и в том случае, если распределение близко к нормальному.
Рекомендации к выбору критерия различий.
При подготовке экспериментального исследования психолог должен заранее запланировать характеристики сопоставляемых выборок (прежде всего связность- несвязность и однородность), их величину (объем), тип измерительной шкалы и вид используемого критерия различий. Последовательно это можно представить в виде следующих этапов [2]:
· Прежде всего, следует определить, является ли выборка связной (зависимой) или несвязной (независимой);
· Следует определить однородность-неоднородность выборки;
· Затем следует оценить объем выборки и, зная ограничения каждого критерия по объему, выбрать соответствующий критерий;
· Если используемый критерий не выявил различия, следует применить более мощный критерий;
· Если в распоряжении психолога имеется несколько критериев, то следует выбирать те из них, которые наиболее полно используют информацию, содержащуюся в экспериментальных данных;
· При малом объеме выборки следует увеличивать величину уровня значимости (не менее 1%, то есть p=0,01), так как небольшая выборка и низкий уровень значимости приводят к увеличению вероятности принятия ошибочных решений.
3.2. Критерий знаков G (непараметрический критерий для связанных выборок)
Для определения достоверности отличий между двумя группами результатов исследования в одной и той же выборке испытуемых, например, «до» и «после» тренинга, используют критерий знаков G.
Для применения критерия G необходимо соблюдать следующие условия:
1. Выборка должна быть однородной и связной.
2. Измерение может быть проведено в шкале порядка, интервалов и отношений.
3. Число элементов в сравниваемых выборках должно быть равным.
4. G критерий знаков может применяться при величине типичного сдвига (большее количество сдвигов по изучаемому признаку) от пяти.
5. При большом числе сравниваемых парных значений критерий знаков достаточно эффективен.
6. При равенстве типичных и нетипичных сдвигов (меньшее количество сдвигов) критерий знаков неприменим, следует использовать другие критерии.
Пример задачи: Исследователь должен выяснить, будет ли эффективен тренинг, направленный на снижение агрессивности у двадцати однокурсников. В качестве оценочного инструмента используется методика диагностики агрессивности А. Ассинера.
Решение: При решении этой задачи (а также и последующих) необходимо уточнить, что с целью сохранения исходных данных исследования лучше всего набрать результаты проведенного эксперимента в программе «Excel», а затем перенести их в программу «Statistica 6.0». Такое решение минимизирует риск потери исходных данных.
После проведения подготовительных работ с документом (см. Приложение 4) он будет выглядеть следующим образом:
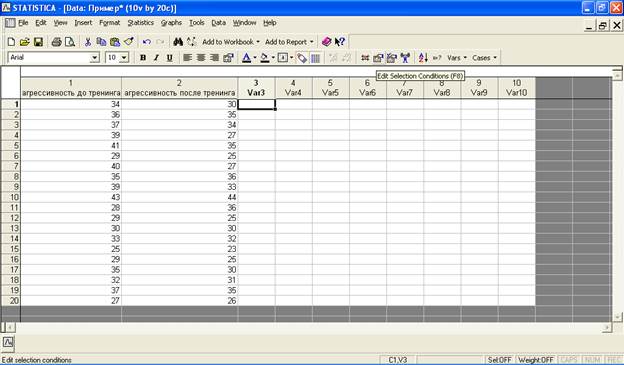
Столбцы документа содержат «сырые» данные тестирования, полученные «до» и «после» проведения тренинга. Перед обработкой данных необходимо определить, соблюдены ли все условия применения критерия знаков G.
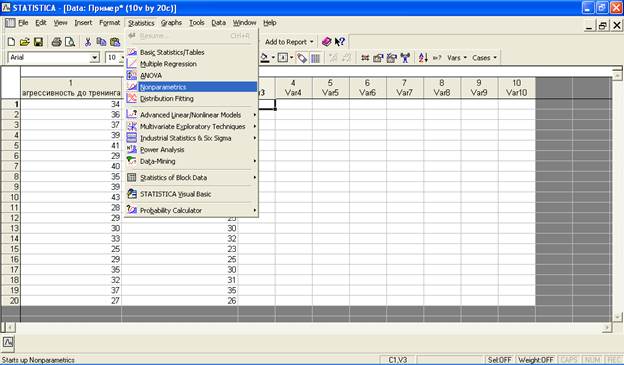
Вверху документа найдите функцию «Statistics» («Статистические функции») и выберите строчку «Nonparametrics» («Непараметрические…»):
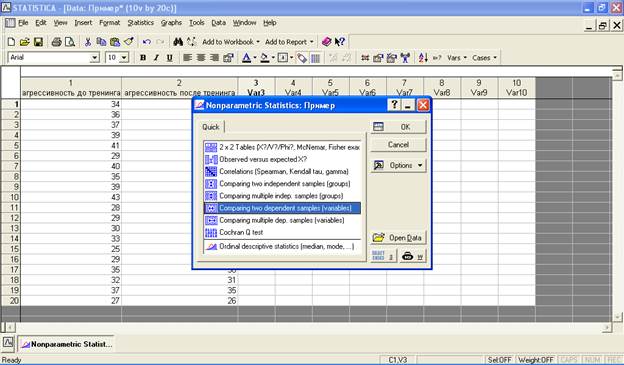
В окне-меню критериев непараметрической статистики нажмите на строчку «Comparing two dependent samples (variables)» («Сравнение двух зависимых выборок»):
В появившемся окне функций непараметрического критерия знаков (Sign test) нажмите на «Variables» («Переменные»):
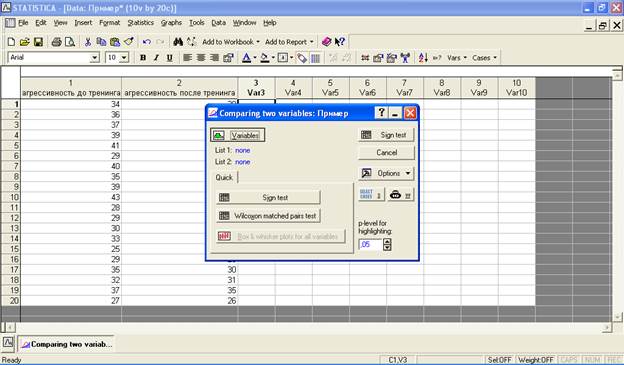
Выберите две сравниваемые группы переменных. В нашем примере в первую группу отнесите значения агрессивности у испытуемых до проведения тренинга, во вторую – после проведения тренинга. Нажмите на «ОК»:
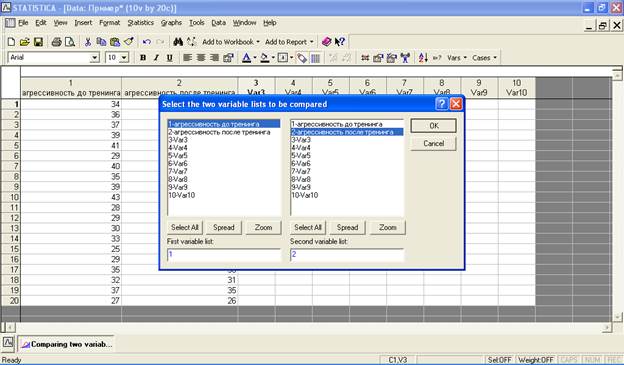
В появившемся окне нажмите на функцию «Sign test» («критерий знаков»):

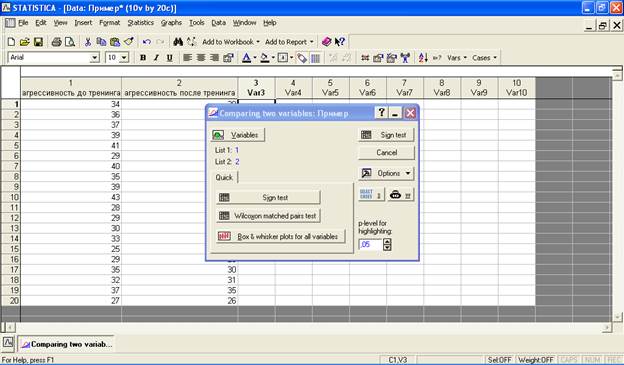
В итоговой статистической таблице выделенные красным цветом показатели свидетельствуют о достоверности различий между значениями двух сравниваемых групп.
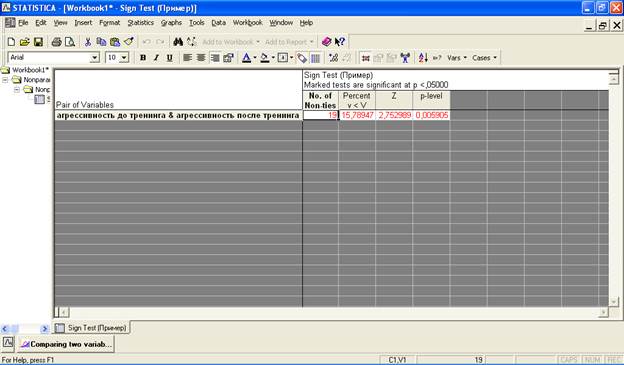
Первый столбец (No. of Non-ties) показывает количество неравенств, то есть изменений в значениях изучаемой переменной. В нашем примере произошло 16 отрицательных изменений (с уменьшением значений переменной), 3 - положительных (с увеличением значений переменной), а также у одного испытуемого не произошло никаких изменений.
Второй столбец (Percent v<V) показывает, сколько в процентном соотношении значений в первой группы меньше значений во второй группе (агрессивность до тренинга < агрессивность после тренинга). В нашем примере около 16 % значений в первой группы оказались меньше, чем во второй, то есть у трех испытуемых после тренинга значения агрессивности увеличились. Таким образом, можно сделать вывод о том, что у 80% (16 человек) испытуемых после участия в тренинге значения агрессивности снизились.
Третий столбец показывает вспомогательную величину (Z) критерия знаков, связанную с функцией стандартного нормального распределения.
Последний четвертый столбец – это показатель p-level (уровень значимости), который является самым важным в данной таблице. По умолчанию в программе «Statistica 6.0» достоверные статистические отличия устанавливаются при значении p-level меньше 0,05.
3.3. Критерий U (непараметрический критерий для несвязанных выборок)
Несвязанные или независимые выборки образуются, когда в целях эксперимента для сравнения привлекаются данные двух или более выборок, причем эти выборки могут быть взяты из одной или из разных генеральных совокупностей. Таким образом, для несвязанных выборок характерно, что в них обязательно входят разные испытуемые.
Для оценки достоверности различий между несвязанными выборками используется ряд непараметрических критериев. Одним из наиболее распространенных является критерий U(Вилкоксона-Манна-Уитни). Этот критерий применяют для оценки различий по уровню выраженности какого-либо признака для двух независимых (несвязанных) выборок. При этом выборки могут различаться по числу входящих в них испытуемых.
Для применения критерия Uнеобходимо соблюдать следующие условия:
1. Выборки должны быть несвязанными.
2. Измерение должно быть проведено в шкале интервалов и отношений.
3. Нижняя граница применимости критерия n1≥3 и n2≥3 или n1≥2, n2≥5.
Пример задачи: Исследователь должен выяснить, отличаются ли отметки за сессию двух учебных групп. Численность обучающихся в каждой группе 15 человек.
Решение: После проведения подготовительных работ с документом (см. Приложение 4) он будет выглядеть следующим образом: в первом столбце («отметка») размещены учебные отметки всех испытуемых, во втором столбце («Код») напротив каждой учебной отметки проставлен код принадлежности испытуемого к одной из двух учебных групп. Значения кодов могут быть любыми, главное, чтобы они не совпадали. Для простоты изложения в нашем примеры код первой учебной группы равен нулю («0»), второй – единицы («1»). Таким образом, учебные отметки испытуемых первой группы соотносятся с кодом «0», а второй – с кодом «1».
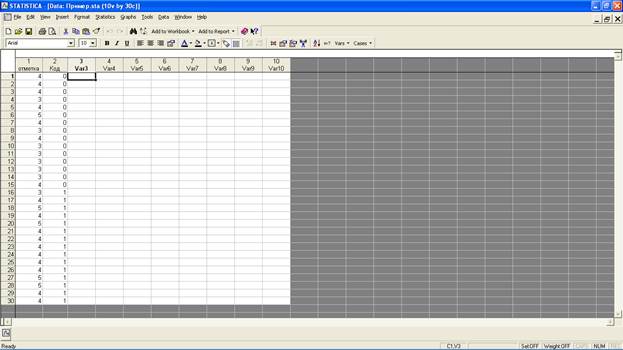
Вверху документа найдите функцию «Statistics» («Статистические функции») и выберите строчку «Nonparametrics» («Непараметрические…»). В окне-меню критериев непараметрической статистики нажмите на строчку «Comparing two independent samples (groups)» («Сравнение двух зависимых выборок»). В появившемся окне функций непараметрического критерия знаков Манна-Уитни (U test) нажмите на «Variables» («Переменные»):
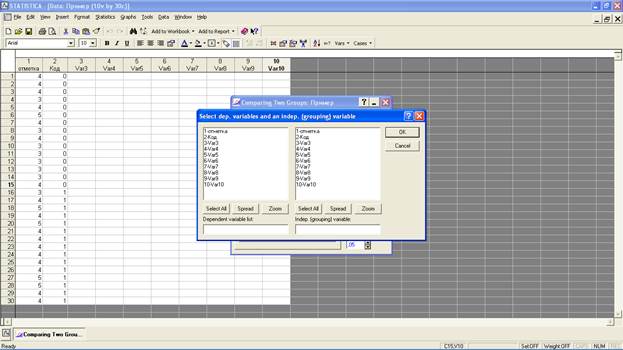
Выберите две группы переменных. В левой нижней части таблицы необходимо обозначить зависимую переменную (dependent variable), которая в нашем примере связана с учебной отметкой, поэтому нажмите на «1-отметка». В правой нижней части таблицы необходимо обозначить независимую переменную (indep. variable), которая в нашем примере связана с участием в исследовании двух учебных групп, выделенных кодами «0» и «1», поэтому нажмите на «2-Код». После окончания работы с данным окном нажмите на «ОК».
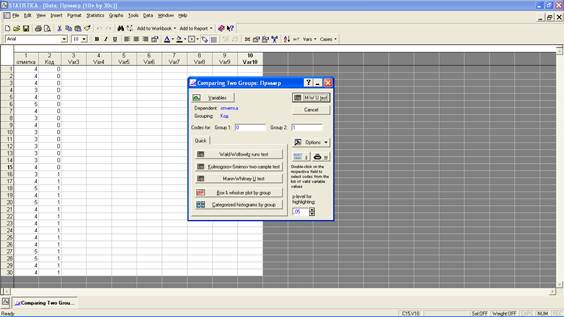
В новом появившемся окне вы увидите, что программа все значения испытуемых первой группы связала с кодом «0», а значения испытуемых второй группы с кодом «1». Нажмите на «M-W U test».


В итоговой статистической таблице выделенные красным цветом показатели свидетельствуют о достоверности различий между значениями двух сравниваемых групп.
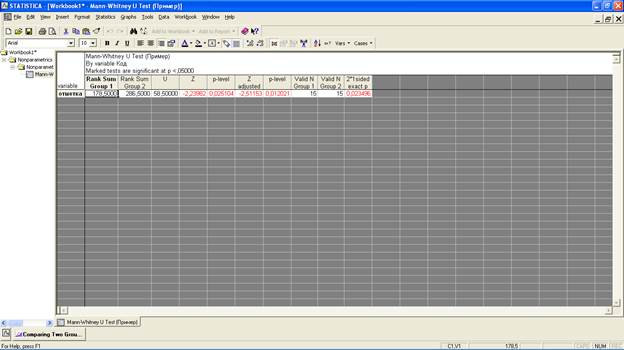
Первый столбец (Rank Sum Group 1) показывает сумму рангов для значений испытуемых первой группы (178,5). Второй столбец (Rank Sum Group 2) показывает сумму рангов для значений испытуемых второй группы (286,5).
Третий столбец показывает значения используемого критерия Манна-Уитни (Uэмп), который в нашем примере равен 58,5.
Четвертый столбец показывает вспомогательную величину (Z) для больших выборок критерия U, связанную с функцией стандартного нормального распределения. Важно отметить, что положительное значение данной величины (Z) свидетельствует о выраженности изучаемой зависимой переменной (учебная отметка) в первой группе испытуемых, отрицательное – во второй.
Пятый столбец – показатель p-level (напомним, что он подчеркивает вероятность принятия гипотезы Н0), который в нашем примере ниже установленного по умолчанию значения 0,05, что свидетельствует о статистически достоверных различиях между учебными отметками двух исследуемых групп.
Шестой и седьмой столбцы показывают скорректированные значения нормального распределения для Z и p-level.
Восьмой и девятый столбцы показывают объем выборки в первой (Valid N Group 1) и во второй (Valid N Group 2) группах.
Последний столбец помогает определить точную вероятность, связанную с соответствующей U статистикой, для выборок малого объема. Эта вероятность основана на подсчете всех возможных значений U при заданном количестве наблюдений в двух выборках. В данном столбце появляется значение 2*p, где p равно 1 минус кумулятивная (односторонняя) вероятность соответствующей U статистики. Заметим, что это обычно не приводит к большой недооценке статистической значимости соответствующих результатов исследования.
Дата добавления: 2016-03-10; просмотров: 11980;
