Примеры применения математико-статистических методов обработки данных в психологических исследованиях
Пример 1.Определим, связаны ли между собой индивидуальные показатели готовности к обучению в центре подготовки операторов, полученные до начала обучения у кандидатов на учебу, и их средняя успеваемость в конце периода обучения с помощью коэффициента ранговой корреляции Спирмена.
Коэффициент корреляции Rs Спирмена вичисляется по формуле:
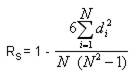 (1)
(1)
где N – количество ранжируемых признаков (показателей, испытуемых);
di – разность между рангами по двум переменным (например, по качеству деятельности и результатам выполнения теста) для каждого испытуемого;
Для решения этой задачи необходимо проранжировать, во-первых, значения показателей готовности к обучению и, во-вторых, итоговые показатели успеваемости в конце периода обучения. Результаты представлены в таблице 1:
Таблица 1
Ранги показателей готовности к обучению и успеваемости операторов
| № кандидата п/п | ||||||||||||
| Ранги показателей готовности | ||||||||||||
| Ранги успеваемости | ||||||||||||
| di | -2 | -2 | -2 | -2 | -2 | |||||||
| di2 |
Полученные данные подставляем в формулу (1) и производим расчет:
Rs = 1 – 6*52/(11(112-1)) = 0,76.
Для нахождения уровня значимости обращаемся к таблице 1 (приложения 3), в которой приведены критические значения для коэффициентов ранговой корреляции. Уровни значимости определяем по числу испытуемых n. В нашем случае n= 11. Тогда для уровня значимости p = 0,05 коэффициент корреляции Rкр1= 0,61 и для уровня значимости p = 0,01 - Rкр2= 0,76.
Полученный коэффициент корреляции совпал с критическим значением для уровня значимости, равного 0,01. Следовательно, можно утверждать, что показатели готовности и итоговые оценки успеваемости связаны положительной корреляционной зависимостью. Иначе говоря, чем выше показатель готовности, тем успешнее будет учиться кандидат. В терминах статистических гипотез необходимо принять гипотезу о наличии взаимосвязи, т.е. связь между показателями готовности и средней успеваемостью отлична от нуля.
Пример 2
Определим, влияет ли уровень интеллекта операторов на их профессиональные достижения с помощью критерия «хи-квадрат».
с помощью критерия «хи-квадрат» Пирсона χ2эмп, устанавливающего степень значимости различия распределений признака, полученных при обследовании двух групп лиц, разделенных по частным или обобщенным показателям профессиональной эффективности или другим прогнозируемым показателям, по формуле:
k
χ2эмп=Σхi2/fmi , (2)
i=1
где хi - разность между эмпирическими и «теоретическими» частотами;
k – количество разрядов признака;
fmi - вычисленная или «теоретическая» частота;
или
n m
χ 2эмп= M{Σ ΣСij2/(CiCj)-1}, (3)
i=1 j=1
где n - число строк многопольной таблицы;
т — число столбцов многопольной таблицы;
M — общее число значений (элементов) в многопольной таблице, вычисляемое по формуле:
M= n∙m; (4)
Cij — элементы многопольной таблицы;
Ci — суммарные значения по строкам многопольной таблицы;
Сj — суммарные значения по столбцам многопольной таблицы
При этом статистическая значимость рассчитываемых показателей должна быть не менее 0,05.
Для применения критерия χ2эмп необходимо соблюдать следующие условия:
- измерение может быть проведено в любой шкале;
- выборки должны быть случайными и независимыми;
- желательно, чтобы объем выборки был > 20. С увеличением объема выборки точность критерия повышается;
- теоретическая частота для каждого выборочного интервала не должна быть меньше 5;
- сумма наблюдений по всем интервалам должна быть равна общему количеству наблюдений;
- таблица критических значений критерия χ2эмп рассчитана для числа степеней свободы v, которое каждый раз рассчитывают по определенным правилам.
В общем случае число степеней свободы вычисляется по формуле:
v = с - 1, (5)
где с — число альтернатив (признаков, значений, элементов) в сравниваемых переменных.
Для таблиц число степеней свободы вычисляют по формуле:
v = (n - 1)(m - 1), (6)
где n— число строк, m — число столбцов.
Первый способ решения - по формуле (2).
Например, 90 человек оценили по степени их профессиональных достижений и по уровню интеллекта. При разбиении на уровни (градации признака) по обоим признакам было взято три уровня. Для показателя профессиональных достижений были получены следующие частоты признака: 20 человек с высоким уровнем профессиональных достижений, 40 - со средним и 30 - с низким. Первая группа составляет 22,2%, вторая — 44,4% и третья — 33,3% от всей выборки. При разбиении по уровню интеллекта было взято три равных по численности группы - по 30 человек: с уровнями интеллекта ниже среднего, средним и выше среднего. Каждая группа составляет 33,3% от всей выборки. Все эмпирические данные (частоты) представлены в таблице 2:
Таблица 2
Частота распределения испытуемых по уровням оцениваемых признаков
| IQ | Оценка профессиональных достижений | Всего | ||
| Ниже среднего | Средняя | Выше среднего | ||
| Ниже среднего | 20 А (10) | 5 S (13,3) | 5 С (6,7) | |
| Средний | 5 D(10) | 15 Е(13,3) | 10 F (6,7) | |
| Выше среднего | 5 G(10) | 20 Н(13,3) | 5 J (6,7) | |
| Итого |
Для удобства каждая ячейка таблицы обозначена соответствующей латинской буквой: А, S, С и т.д. Таблица 2 устроена следующим образом: в ячейку, обозначенную символом А, заносят эмпирические частоты (или число) тех испытуемых, которые одновременно обладают характеристикой: ниже среднего по уровню профессиональных достижений и ниже среднего по интеллекту. Таких испытуемых (эмпирических частот) оказалось 20. В ячейку, обозначаемую символом S, заносят эмпирические частоты (или число) тех испытуемых, которые одновременно обладают характеристикой: средние по уровню профессиональных достижений и ниже среднего по интеллекту. Таких испытуемых (эмпирических частот) оказалось 5. В ячейку, обозначенную символом С, заносят эмпирические частоты (или число) тех испытуемых, которые одновременно обладают характеристикой: выше среднего по уровню профессиональных достижений и ниже среднего по интеллекту. Таких испытуемых (эмпирических частот) оказалось также 5. Заметим, что 20 + 5 + 5 = 30, т.е. числу испытуемых, имеющих уровень интеллекта ниже среднего. Подобные «разбиения» были проделаны для каждой ячейки таблицы 2. В круглых скобках в каждой ячейке таблицы представлены вычисленные для этой ячейки «теоретические» частоты.
Покажем, как для каждой ячейки таблицы 2 найти соответствующую «теоретическую» частоту. Для этого для каждого столбца таблицы подсчитывают так называемые «частости» в процентах:
30/90∙100 % = 33,3%;
40/90∙100 % = 44,4%;
20/90∙100 % = 22,2%.
Полученные величины «частостей» дают возможность подсчитать «теоретические» частоты для каждой ячейки. Они служат основой для подсчета «гипотетических» (а по сути теоретических) частот, т.е. таких, которые при заданном соотношении экспериментальных данных должны были бы быть расположены в соответствующих ячейках таблицы 2.
Согласно этому положению «теоретическую» частоту для ячейки А подсчитывают следующим образом. 30 человек имеют уровень интеллекта ниже среднего, поэтому 33,3 % от этого числа должны были бы попасть в группу с профессиональными достижениями ниже среднего уровня. Находим эту «гипотетическую» величину: 30*33,3%/100%∙= 9,99 ≈ 10.
Аналогично подсчитывают «теоретические» частоты для ячеек D,G,S,E,H,C,F и J.
Проверка правильности расчета «теоретических» частот для всех столбцов таблицы А.2 проводят следующим образом: 10 + 10 + 10 = 30; 13,3 + 13,3 + 13,3 = 39,9 ≈ 40; 6,7 + 6,7 + 6,7 = 20,1 ≈ 20.
Для проверки правильности расчета «теоретических» частот в случае сравнения двух эмпирических наблюдений или для сравнения показателей внутри одной выборки может использоваться следующая формула:
fCij = Σfi*Σfj/K, (7)
где fCij – теоретическая частота в соответствующей ячейке многопольной таблицы;
Σfi – сумма эмпирических частот по строке;
Σfj – сумма эмпирических частот по столбцу;
K – общее количество наблюдений.
Теперь используем формулу (2):
χ 2эмп = (20-10)2/10+(5-13,3)2/13,3+(5-6,7)2/6,7+(5-10)2/10+(15-13,3)2/13,3+(10-6,7)2/6,7+(5-10)2/10+(20-13,3)2/13,3+(5-6,7)2/6,7=26,5
Число степеней свободы подсчитаем по формуле (6):
v = (n - 1)(m - 1) = (3 - 1)(3 - 1) = 4.
В соответствии с таблицей 3 (приложение 1):
χ 2кр1 = 9,49 для p≤0,05 и χ 2кр2 = 13,28 для p≤0,01
Полученная эмпирическая величина критерия «хи-квадрат» χ 2эмп = 26,5 попадает в зону значимости, т.е. χ 2эмп> χ 2кр2(p≤0,01). Иными словами, следует принять гипотезу о том, что уровень интеллекта влияет на успешность профессиональной деятельности.
Второй способ решения - по формуле (3).
Подставив данные таблицы 2 в формулу (3), получим:
χ 2эмп = 90(1/30(202/30+52/40+52/20)+1/30(52/30+152/40+102/20)+ 1/30(52/30+202/40+52/20)-1) = 90(1/2+13/24+1/4-1) = 26,5
Как и следовало ожидать, эмпирическое значение «хи-квадрат» получено то же самое, что и при первом способе решения. Все дальнейшие операции уже проделаны выше при первом способе решения данной задачи. Второй способ существенно проще первого, однако при расчетах по формуле (3) можно легко допустить ошибки. Как первый, так и второй способы расчета эмпирического значения «хи-квадрат» позволяют работать с таблицами практически любой размерности: 3x4, 4x4, 5x3, 5х6 и т.п.
Приложение 4
Дата добавления: 2016-03-10; просмотров: 993;
