Примеры приложения теоремы Кастильяно.

Определим (Рис.4) прогиб свободного конца В балки, защемленной другим концом А. Балка нагружена сосредоточенной силой, приложенной в точке В. В данном случае возможно непосредственное применение теоремы Кастильяно, так как отыскивается прогиб сечения, где приложена сосредоточенная сила Р

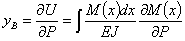
Рис.4. Пример расчетной схемы для расчета перемещений.

Начало отсчета абсциссы х сечения можно выбирать произвольно, лишь бы формула для М (х) была возможно проще. Отсчитывая х от точки В, получаем для момента в любом сечении балки

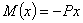и

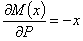
Подставляя эти значения в формулу для 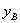и интегрируя, чтобы охватить всю длину балки от 0 до l, получаем:

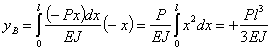
Лекция № 34. Теоремы о взаимности работ и Максвелла — Мора.

Пользуясь понятием о потенциальной энергии, можно установить следующую зависимость между деформациями в различных сечениях балки.

Если к балке, нагруженной силой 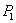приложить затем статически силу 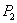в сечении 2, то к прогибу точки приложения силы 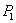от этой же силы 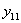прибавится (Рис.1) прогиб от силы 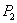, равный 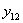; первый значок у буквы у указывает точку, для которой вычисляется прогиб; второй — обозначает силу, вызывающую этот прогиб.

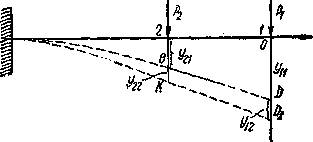
Рис.1. Расчетная схема к теореме о взаимности работ

Полная работа внешних сил составится из трех частей: работы силы 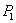на вызванном ею прогибе 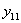, т. е. 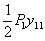, работы силы 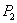на вызванном ею прогибе ее точки приложения 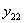, т. е. 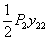, наконец, работы силы 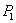на прогибе ее точки приложения от силы 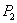, т. е. .

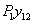Таким образом, накопленная в стержне при действии обеих сил энергия будет равна:

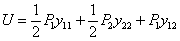
Это количество энергии деформации зависит лишь от конечных значений сил и прогибов и не зависит от порядка нагружения.

Если к балке, загруженной силой 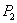, приложить затем силу 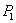то, повторив цепь вычислений, получим:

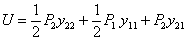
Сравнивая оба значения U, получаем:

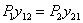
т. е. работа силы 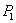(или первой группы сил) на перемещениях, вызванных силой 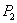(второй группой сил), равна работе силы 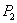на перемещениях, вызванных силой .

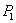Это и есть теорема о взаимности работ. Ее можно сформулировать и иначе: работа первой силы ( 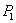) при действии второй ( 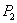) равна работе второй силы при действии первой.