Общие понятия и метод расчета.
До сих пор мы рассматривали только статически определимые балки, у которых три опорные реакции определялись из условий равновесия. Очень часто, по условиям работы конструкции, оказывается необходимым увеличить число опорных закреплений; тогда мы получаем так называемую статически неопределимую балку.
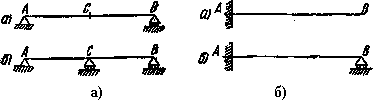
Рис.1. Схемы статически неопределимых балок
Например, для уменьшения пролета балки АВ на двух опорах (Рис.1, а) можно поставить опору еще посредине, а для уменьшения деформаций балки, защемленной одним концом (Рис.1, б), можно подпереть ее свободный конец.
Для подбора сечения таких балок, так же как и в рассмотренных ранее задачах, необходимо построить обычным порядком эпюры изгибающих моментов и поперечных сил, а стало быть, определить опорные реакции.
Во всех подобных случаях число опорных реакций, которые могут возникнуть, превышает число уравнений статики, например, для балок рис.2. Соответственно: четыре, четыре и пять опорных реакций.

Рис.2. Механизм появления дополнительных связей
Поэтому необходимо составить дополнительные уравнения, выражающие условия совместности деформаций, которые вместе с обычными уравнениями равновесия и дадут возможность определить все опорные реакции.
Определим опорные реакции и построим эпюру моментов для балки, находящейся под действием равномерно распределенной нагрузки q рис.3. Сначала изобразим все реакции, которые по устройству опор могут возникнуть в этой балке. Таких реакций может быть на опоре А три: вертикальная А, горизонтальная 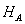 и опорный момент
и опорный момент 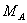 , на опоре В возможно появление лишь одной реакции В. Таким образом, число опорных реакций на одну больше, чем уравнений статики.
, на опоре В возможно появление лишь одной реакции В. Таким образом, число опорных реакций на одну больше, чем уравнений статики.
Одна из реакций является добавочной, как говорят, «лишней» неизвестной. Этот термин прочно укоренился в технической литературе; между тем, принять его можно лишь условно.

Рис.3. Исходная расчетная схема статически неопределимой балки.
Действительно, добавочная реакция и соответствующее ей добавочное опорное закрепление являются «лишними» только с точки зрения необходимости этих закреплений для равновесия балки как жесткого целого. С точки же зрения инженера добавленное закрепление во многих случаях не только не является лишним, а наоборот, позволяет осуществить такую конструкцию, которая без него была бы невозможна. Поэтому мы будем пользоваться термином «лишняя опорная реакция», «лишняя неизвестная» лишь условно.
Составим все уравнения статики для нашей балки, приравнивая нулю сумму проекций всех сил на направление оси балки, на перпендикуляр к ней, и сумму моментов относительно точки А. Получим систему:
 ,
, 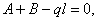
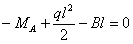
Из первого уравнения сразу определяется опорная реакция 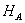 Для определения трех других остаются лишь два уравнения.
Для определения трех других остаются лишь два уравнения.
За лишнюю реакцию можно взять любую из этих трех: попробуем взять реакцию опоры В. В таком случае мы должны считать, что рассматриваемая балка получилась из статически определимой балки АВ, защемленной концом А, у которой потом поставили добавочную опору в точке В. Эта статически определимая балка, которая получается из статически неопределимой при удалении добавочного, лишнего опорного закрепления, называется основной системой. Выбрав какую-либо из реакций за лишнюю неизвестную, мы тем самым выбираем основную систему.
Попробуем теперь превратить основную систему без опоры В в систему, полностью совпадающую с заданной статически неопределимой балкой (Рис.3).

Рис.4. Эквивалентная система
Для этого загрузим ее сплошной нагрузкой q и в точке В приложим лишнюю реакцию В (Рис.4).
Однако этого мало: в балке, представленной на рис.4, точка В может перемещаться по вертикали под действием нагрузок q и В; между тем, в нашей статически неопределимой балке точка В не имеет этой возможности, она должна совпадать с опорным шарниром. Поэтому, чтобы привести к окончательному совпадению, надо к последней добавить условие, что прогиб точки В основной системы под действием нагрузок q и В должен быть равен нулю:
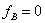
Это и будет добавочное уравнение, определяющее реакцию В; оно является условием совместности деформаций в рассматриваемом случае: конец В балки не отрывается от опоры.
Решение этого добавочного уравнения возможно несколькими способами.
Дата добавления: 2016-03-05; просмотров: 698;
