Теорема Максвелла—Мора.
Прогиб балки в точке приложения сосредоточенной силы Р равен:
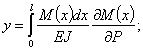
аналогичное выражение мы имеем и для угла поворота с заменой производной 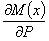 на
на 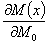 . Выясним, что представляют собой эти производные.
. Выясним, что представляют собой эти производные.
Если на балке расположена какая угодно нагрузка из сосредоточенных сил 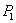 ,
, 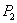 ,
, 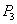 ,..., моментов
,..., моментов 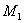 ,
, 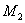 ,..., сплошных нагрузок
,..., сплошных нагрузок 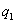 ,
, 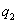 ..... то момент М(х) в любом сечении такой балки выражается линейной функцией от нагрузок:
..... то момент М(х) в любом сечении такой балки выражается линейной функцией от нагрузок:
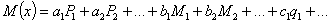

Рис.2. Частная расчетная модель метода Максвелла — Мора.
Коэффициенты 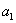 ,
, 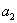 ,...,
,..., 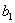 ,
, 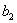 …,
…, 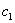 ,
, 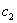 ... являются функциями пролета балки, расстояний точек приложения сил и моментов от опор и абсциссы х взятого сечения. Пусть мы отыскиваем прогиб точки приложения силы
... являются функциями пролета балки, расстояний точек приложения сил и моментов от опор и абсциссы х взятого сечения. Пусть мы отыскиваем прогиб точки приложения силы 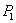 ; тогда
; тогда
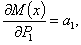
так как 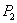 ,
, 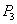 ,...,
,..., 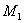 ,
, 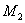 ,...,
,..., 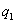 ,
, 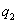 ...,
..., 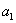 ,
, 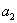 ,...,
,..., 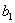 ,
, 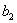 …,
…, 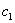 ,
, 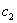 ... при этом дифференцировании постоянны. Но
... при этом дифференцировании постоянны. Но 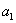 можно рассматривать как численную величину момента М в любом сечении балки от действия так называемой единичной нагрузки, т. е. силы
можно рассматривать как численную величину момента М в любом сечении балки от действия так называемой единичной нагрузки, т. е. силы 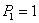 ; действительно, подставляя в формулу вместо
; действительно, подставляя в формулу вместо 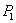 его частное значение, единицу, и приравнивая все остальные нагрузки нулю, получаем
его частное значение, единицу, и приравнивая все остальные нагрузки нулю, получаем 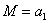 .
.
Например, для балки, изображенной на Рис2, а, изгибающий момент равен:
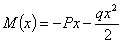
Производная 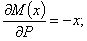 ; но это как раз и будет выражение изгибающего момента нашей балки, если мы ее нагрузим силой 1, приложенной в той же точке В, где расположена сила Р (Рис.2, б), и направленной в ту же сторону.
; но это как раз и будет выражение изгибающего момента нашей балки, если мы ее нагрузим силой 1, приложенной в той же точке В, где расположена сила Р (Рис.2, б), и направленной в ту же сторону.
Аналогично, производная изгибающего момента М (х) по паре сил 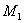 численно представляет собой изгибающий момент от пары с моментом, равным единице, приложенной в том же сечении, где имеется пара
численно представляет собой изгибающий момент от пары с моментом, равным единице, приложенной в том же сечении, где имеется пара 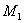 , и направленной в ту же сторону. Таким образом, вычисление производных изгибающего момента можно заменить вычислением изгибающих моментов от единичной нагрузки. Эти моменты мы будем обозначать буквой
, и направленной в ту же сторону. Таким образом, вычисление производных изгибающего момента можно заменить вычислением изгибающих моментов от единичной нагрузки. Эти моменты мы будем обозначать буквой 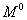 .
.
Таким образом, для отыскания перемещения 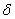 (прогиба или угла поворота) любого сечения балки, вне зависимости от того, приложена или не приложена в этом сечении соответствующая сила, необходимо найти выражение для изгибающего момента М от заданной нагрузки и момента
(прогиба или угла поворота) любого сечения балки, вне зависимости от того, приложена или не приложена в этом сечении соответствующая сила, необходимо найти выражение для изгибающего момента М от заданной нагрузки и момента 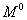 от соответствующей единичной нагрузки, приложенной в сечении, где ищем перемещение
от соответствующей единичной нагрузки, приложенной в сечении, где ищем перемещение 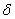 ; тогда это перемещение выразится формулой
; тогда это перемещение выразится формулой
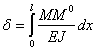
Эта формула была предложена Максвеллом в 1864 г. и введена в практику расчета О. Мором в 1874 г. Если мы в полученном выражении под 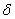 подразумеваем прогиб, то момент
подразумеваем прогиб, то момент 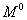 надо вычислять от сосредоточенной единичной силы, приложенной в той точке, где мы отыскиваем прогиб; при вычислении же угла поворота в качестве единичной нагрузки прикладывается пара сил с моментом, равным единице.
надо вычислять от сосредоточенной единичной силы, приложенной в той точке, где мы отыскиваем прогиб; при вычислении же угла поворота в качестве единичной нагрузки прикладывается пара сил с моментом, равным единице.
Для примера рис.2 имеем:
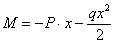
| (рис.2,а) |
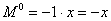
| (рис.2, б) |
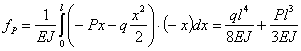
Знак плюс означает, что направление перемещения совпадает с направлением единичной нагрузки, знак минус — наоборот.
Если при определении изгибающих моментов придется делить балку на участки, то соответственно и интеграл в формуле распадется на сумму интегралов.
Сравнивая формулу Кастильяно с формулой Мора, нетрудно заметить, что они отличаются лишь одним множителем. В теореме Кастильяно 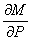 или
или 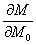 , в теореме Мора
, в теореме Мора 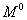 .
.
Следовательно, производная от изгибающего момента по обобщенной силе — это то же самое, что изгибающий момент от силы 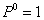 .
.
Метод Верещагина.
Способ Максвелла — Мора в значительной степени вытеснил на практике непосредственное применение теоремы Кастильяно. В справочниках обычно приводятся таблицы интегралов 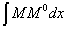 для наиболее часто встречающихся типов нагрузки.
для наиболее часто встречающихся типов нагрузки.
Наш соотечественник А. Н. Верещагин в 1924 г. предложил упрощение вычислений. Так как единичной нагрузкой бывает обычно либо сосредоточенная сила, либо пара сил, то эпюра 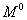 оказывается ограниченной прямыми линиями. Тогда вычисление
оказывается ограниченной прямыми линиями. Тогда вычисление 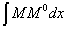 при любом очертании эпюры М можно произвести следующим образом. Пусть эпюра М (Рис.3) имеет криволинейное очертание, а эпюра
при любом очертании эпюры М можно произвести следующим образом. Пусть эпюра М (Рис.3) имеет криволинейное очертание, а эпюра 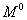 — прямолинейное. Произведение Mdx можно рассматривать, как элемент
— прямолинейное. Произведение Mdx можно рассматривать, как элемент 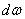 площади эпюры М, заштрихованный на чертеже.
площади эпюры М, заштрихованный на чертеже.
Так как ордината 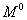 равна
равна 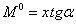 , то произведение
, то произведение 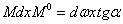 , а весь интеграл
, а весь интеграл 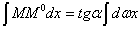 представляет собой статический момент площади эпюры М относительно точки А, умноженный на
представляет собой статический момент площади эпюры М относительно точки А, умноженный на 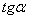 .
.
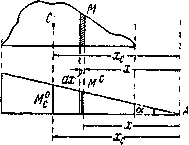
Рис.3. Расчетная модель метода Верещагина.
Но этот статический момент равен всей площади 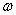 эпюры М, умноженной на расстояние от ее центра тяжести
эпюры М, умноженной на расстояние от ее центра тяжести 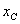 до точки А. Таким образом,
до точки А. Таким образом,
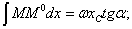
но величина 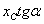 равна ординате
равна ординате 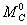 эпюры
эпюры 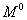 под центром тяжести эпюры М. Отсюда
под центром тяжести эпюры М. Отсюда
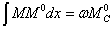
и искомое перемещение равно
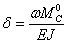
Таким образом, для определения перемещения 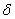 надо вычислить
надо вычислить 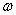 — площадь эпюры М, умножить ее на ординату
— площадь эпюры М, умножить ее на ординату 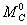 эпюры от единичной нагрузки под центром тяжести площади
эпюры от единичной нагрузки под центром тяжести площади 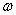 и разделить на жесткость балки.
и разделить на жесткость балки.
Определим этим способом угол поворота сечения D балки, изображенной на Рис.4, а; Балка загружена моментом М, приложенным в сечении В к консоли АВ. Эпюра М показана на Рис.4, б. Прикладываем в сечении D единичную пару, выбирая ее направление произвольно (Рис.4, в). Эпюра моментов от единичной нагрузки показана на рис.4, г. Так как М на участках DC и СВ равен нулю, то остается лишь один интеграл для участка АВ.
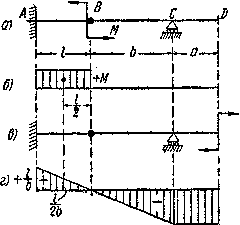
а) расчетная схема б)грузовая эпюра в)фиктивное состояние г) эпюра моментов от единичного момента
Рис.4. Иллюстрация метода Верещагина:
Площадь 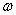 равна
равна 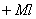 ; ордината эпюры
; ордината эпюры 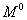 под центром тяжести площади
под центром тяжести площади 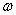 равна
равна 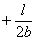 отсюда искомый угол поворота
отсюда искомый угол поворота 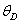 равен
равен
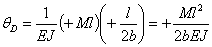
Знак плюс показывает, что вращение происходит по направлению единичной пары, т. е. по часовой стрелке.
Лекция № 35. Расчет статически неопределимых балок. Способ сравнения деформаций.
Дата добавления: 2016-03-05; просмотров: 759;
