Расчет зубьев на изгибную прочность

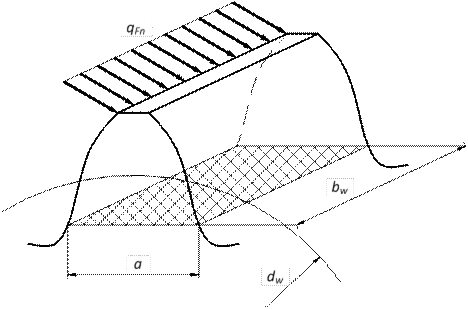Рис. 4.10

Наибольшие нормальные напряжения от изгиба в одном из сопряженных зубьев возникают в начальный момент их зацепления. Зуб рассматривается как консольная балка, нагруженная удельной силой нормального давления (распределенной нагрузкой) q_Fn с опасным сечением размерами a×b_w у основания (рис. 4.10). Зуб представляет собой короткую и широкую консоль, размеры опасного сечения которой соизмеримы с ее длиной. В таких случаях при изгибе возникает поворот и депланация сечений, т.е. гипотеза плоских сечений не соблюдается. Определение напряжений в таких случаях связано с решением сложной пространственной задачи теории упругости.

Для получения достаточно простых зависимостей, используемых в инженерных расчетах, нормальные напряжения будем определять в соответствии с классической теорией изгиба. При этом погрешности, которые вносит теория в решение задачи, компенсируются введением в расчет ряда опытных коэффициентов. Все величины, входящие в расчетные формулы, выразим через параметры ведущего колеса – шестерни.

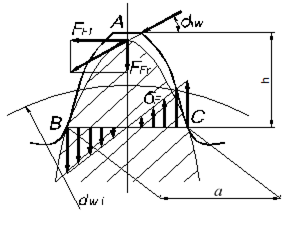Рис. 4.11

Рассмотрим зуб, нагруженный силой нормального давления F_n (рис. 4.11). Перенесем силу F_n по линии ее действия в точку А и разложим на две составляющие – окружное усилие F_t и радиальное усилие F_r. Для определения опасного сечения в зуб впишем профиль балки равного сопротивления, который очерчивается квадратичной параболой с вершиной в точке А. В точках В и С, где ветви параболы касаются эвольвент бокового профиля зуба, нормальные напряжения изгиба имеют наибольшие значения.

Напряжения от составляющей F_r= F_nsinα_w составляют 4-6 % от напряжения изгиба, поэтому ими можно пренебречь.

В соответствии с классической теорией плоского изгиба нормальные напряжения определяются по формуле:

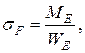(4.27)

где M_E – изгибающий момент:

M_И=F_th. (4.28)

Здесь примем:

F_t = 2 T/d_w1, (4.29)

W_E – момент сопротивления изгибу опасного сечения:

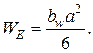(4.30)

С учетом (4.28) и (4.29) запишем формулу для определения напряжений изгиба в виде:

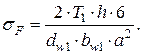(4.31)

Обозначим α= α₁·p_t, h= α₂·p_t, где p_t – окружной шаг, α₁ и α₂ – численные коэффициенты. Введем в формулу коэффициент концентрации напряжений у основания зуба K_T. Линейные величины имеют размерность миллиметры, крутящий момент T₁ – ньютонометры, поэтому T₁ помножим на 10³. С учетом того, что p_t=π·m, преобразуем формулу (4.31):

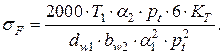(4.32)

Обозначим через Y_F1 коэффициент формы зуба шестерни:

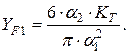(4.33)

Введем в формулу коэффициент нагрузки K_F, аналогичный коэффициенту K_H, который учитывает влияние точности изготовления передачи:

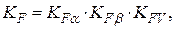, (4.34)

где K_Fα – коэффициент, учитывающий распределение нагрузки между зубьями; K_Fβ – коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца; K_FV – коэффициент, учитывающий динамическую нагрузку в зацеплении.

С учетом принятых обозначений из (4.32) получаем формулу для проверочного расчета зубьев шестерни цилиндрической передачи на прочность по напряжениям изгиба:

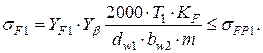(4.35)

В формуле (4.35) σ_FP1 – допускаемое напряжение изгиба зуба шестерни; σ_FP1 – расчетное напряжение зуба шестерни; Y_β – коэффициент, учитывающий наклон зубьев.

Для прямозубой передачи Y_β=1, для косозубой Y_β рассчитывается по зависимости:

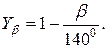(4.36)

Формула проверочного расчета зубчатого колеса на изгибную прочность запишется в виде:

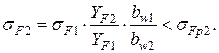(4.37)

Учитывая, что 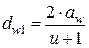, из (4.35) получим формулу для предварительного расчета модуля из условия изгибной прочности:

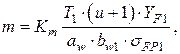(4.38)

где K_m=1400 для прямозубой передачи.

В предварительном расчете коэффициент формы зуба принимается 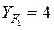для прямозубых колес.