Расчеты на прочность цилиндрических косозубых и шевронных передач
Прочность зуба определяют его размеры и форма в нормальном сечении. Форму косого зуба в этом сечении принято определять через параметры эквивалентного прямозубого колеса. Профиль зуба эквивалентного колеса соответствует профилю зуба косозубого колеса в его нормальном сечении.
Рассечем косозубое колесо нормальной к рабочей поверхности зуба плоскостью n-n (рис. 4.14). В сечении получим эллипс с полуосями а и с. Проведем окружность радиусом ρ, равным радиусу кривизны эллипса в точке k. Эту окружность примем за делительную эквивалентного прямозубого колеса, к расчету которого сводится расчет рассматриваемого косозубого. Все величины, относящиеся к эквивалентному колесу, условимся обозначать с индексом “v”. Установим связь между величинами, относящимися к прямозубому и косозубому колесам.
Радиус кривизны эллипса в точке k:
 .
.
Полуоси эллипса:

откуда:

Ширина bwv и диаметр dv делительной окружности зубчатого венца эквивалентного колеса соответственно равны 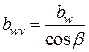 .
.
Поскольку  , то
, то 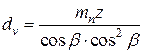 , откуда приведенное число зубьев эквивалентного колеса равно
, откуда приведенное число зубьев эквивалентного колеса равно

Крутящий момент на эквивалентном колесе равен:

С учетом того что 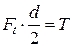 ,
,
где Т – расчетный крутящий момент на косозубом колесе, получим

Подставим значения dwv, awv, bwv, Tv в ранее полученные формулы для проектного и проверочного расчетов прямозубых цилиндрических колес. При этом примем среднее значение коэффициента перекрытия εα=1,7; угла наклона зуба β=12° и коэффициент формы зуба будем определять с учетом приведенного числа зубьев zv. После преобразования получим формулы, которые используют при расчете стальных косозубых колес с углом β=8..16°
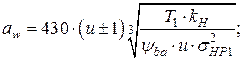 (4.43)
(4.43)
 (4.44)
(4.44)
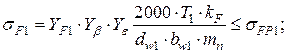 (4.45)
(4.45)
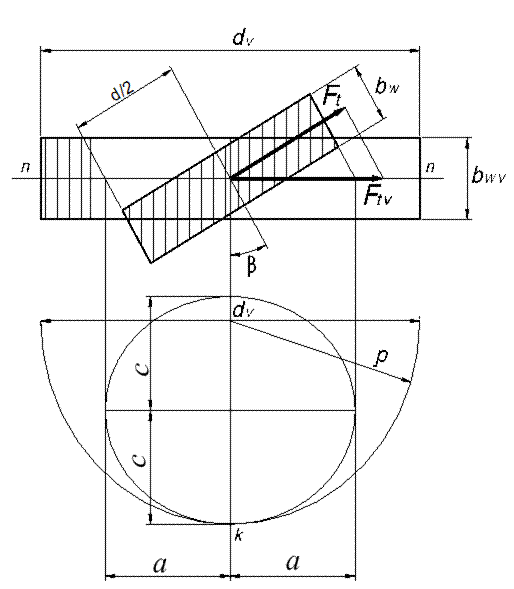 Рис. 4.15
Рис. 4.15
|
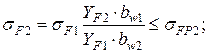 (4.46)
(4.46)
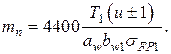 (4.47)
(4.47)
Здесь Yβ коэффициент, учитывающий наклон зубьев, Yε – коэффициент, учитывающий перекрытие зубьев:

Здесь εα – коэффициент перекрытия передачи.
Дата добавления: 2016-03-05; просмотров: 838;
