Комбинативные классификации

Комбинативные (фасетные) классификации возникают как результат классификации понятий по совокупности имен и значений их признаков.

Фасеты такой классификации определяются булевыми операциями над именами признаков и образуют булеву алгебру. Очевидно, что классификацию текстов на основании содержащихся в них дескрипторов с этой точки зрения можно рассматривать как однофасетную, так как мы имеем только один признак ДЕСКРИПТОР для всех терминов, используемых при классификации текстов. Но в комбинативных классификациях, как правило, полагают, что классификационные признаки сущностей не являются множественными.

Для выделения таксонов каждый фасет в свою очередь подвергается дополнительному делению на основе использования значений признаков. Так, если имеются признаки А, В, С, то в комбинативной классификации можно выделить три фасета первого уровня – F^A, F^B, F^C; три фасета второго уровня – F^AB, F^AC, F^BC и один фасет третьего уровня F^ABC. Таксоны первого уровня Т₁^A, T₂^A,…,T_n^A, T₁^B,..., Т_m^B, Т₁^C,... образуются путем деления каждой из фасет F^A, F^B, F^C на основе значений признаков. Таксоны второго уровня могут быть получены путем попарных пересечений таксонов первого уровня и т.д. Количество таксонов на первом уровне определяется суммарной мощностью доменов значений признаков

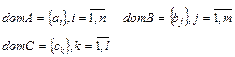
Общее число уровней в комбинативной классификации равно количеству признаков.

Как видно из рис. 6, структура таксонов комбинативной классификации по отношению включения не является иерархической. Если рассматривать структуру связей между отдельными фасетами, то получим булеву алгебру.

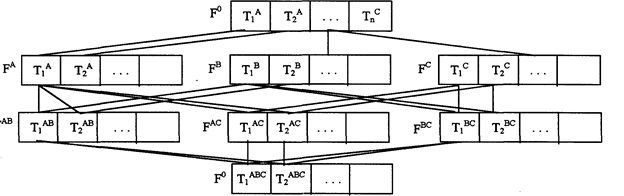
Рис. 6. Фасетная классификационная система

Архетипы классов комбинативной классификации представляют собой подмножество множества пар {(А_i, а_jⁱ)} имен и значений признаков. Для рассмотренного выше примера архетипами классов второго уровня будут множества:

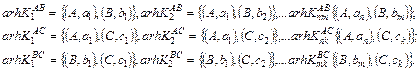
В качестве примера рассмотрим комбинативную классификацию множества сущностей {e₁, e₂, е₃, e₄, e₅, e₆, e₇, e₈}, содержащих признаки с именами А, В, С, D и значениями dom А = {a₁, а₂, а₃}, dom В = {b₁, b₂}, dom С = {c₁, c₂, c₃} и dom D = {d₁, d₂, d₃, d₄}.

Пусть значения признаков по сущностям распределены следующим образом:

e₁ = (a₁, b₁, c₁, d₁), е₂ = (a₁, b₁, c₂, d₁),

е₃ = (a₁, b₂, c₁, d₃), е₄ = (a₁, b₃, c₂, d₃),

e₅ = (а₂, b₂, c₁, d₄), е₆ = (а₂, b₃, c₁, d₄),

е₇ = (а₂, b₃, c₂, d₄), e₈ = (а₂, b₃, c₁, d₂).

Тогда классификационная решетка рассматриваемой предметной области может быть представлена в виде рис. 7. На первом уровне решетки находятся таксоны, которые определяются одиночными значениями признаков, на втором - они определяются парными комбинациями признаков, на третьем - тройками значений признаков.

Таксон Т₀ содержит сущности, принадлежащие всей ПО, так как на него не накладывается никаких ограничений, а таксон T^ABCD пуст вследствие того, что в ПО отсутствуют сущности, обладающие всеми допустимыми значениями признаков одновременно. Отметим также, что в классификационной решетке отсутствуют классы сущностей первого уровня со значениями свойств b₁ и b₂, так как о множествах объектов {e₁, e₂} и {е₃, e₅} можно сделать более точное утвержцение, чем то, что эти классы сущностей обладают свойствами b₁ и b₂. Действительно, таксон T₁ содержит сущности, обладающие как признаком b₁, так и признаком a₁, а таксон T₁ – сущности, имеющие признаки b₂ и C₁. Множества {e₁, e₂} и {е₃, е₅}, выделенные на основании только одного признака b₁ или b₂, являются не классами, а предклассами. При свершении некоторых событий предклассы могут переходить в класс и, наоборот, классы могут превращаться в предклассы.

Отметим, что третий уровень классификационной решетки фактически содержит информацию, совпадающую с признаками ПО, за исключением таксона Т₆, в который попали сущности e₆ и e₈, не различимые на основании классификационных признаков с именами А, В и С, но имеющие различные характеристические признаки: сущность e₆ имеет свойство d₄, а сущность e₈ – признак d₂.

В работе показано, что для рассматриваемого множества таксонов классификационной решетки могут быть выделены таксоны - образующие, позволяющие путем выполнения над ними теоретико-множественной операции пересечения получить все остальные таксоны решетки.

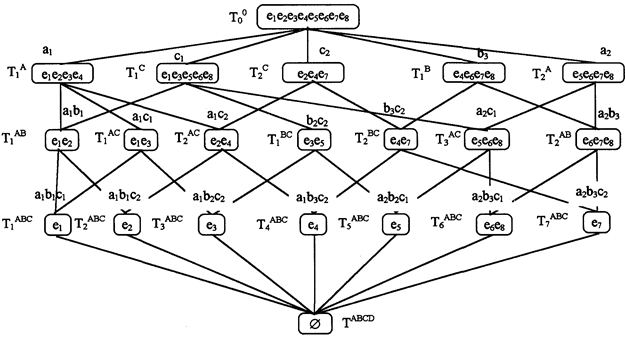
Рис. 7. Пример классификационной решетки гипотетической ПО

Из рис. 7 видно, что в качестве классов-образующих для классификационной решетки необходимо взять таксоны T₁^A, T₁^C, Т₂^C, T₁^B, Т₂^A, T₁^AB, T₁^BC.

Очевиден и общий алгоритм выделения классов-образующих. Для этого достаточно к классам первого уровня решетки присоединить те классы более низких уровней, которые получены из предклассов первого уровня, чтобы получить искомый класс.

Комбинативные классификации имеют ряд преимуществ перед иерархическими классификациями, обеспечивая многоаспектное классифицирование информации, возможность произвольного комбинирования классификационных признаков, большую глубину понятий и возможность гибкого включения новых признаков.

СОБЫТИЯ И ПРОЦЕССЫ