Оценка случайной погрешности результатов измерений

Случайная погрешность проявляется в том, что результаты нескольких равноточных измерений отличаются друг от друга. Теория вероятностей устанавливает, что при n →∞ алгебраическая сумма отклонений при симметричном законе распределения вероятности стремится к нулю:

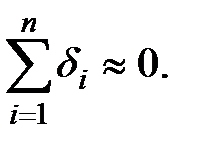
При этом среднее арифметическое значение (математическое ожидание) величины приближается к ее истинному значению. Среднее арифметическое является состоятельной, несмещенной и эффективной оценкой истинного значения:

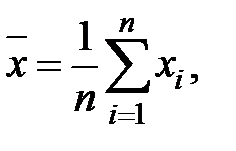(1.17)

где x_i – результаты измерений ФВ; n – число измерений.

При оценке случайной погрешности обычно предполагается, что распределение ее величины описываются формулой Гаусса (нормальный закон распределения), рис. 1.5. Далее будем полагать, что распределение случайных погрешностей подчинено именно нормальному закону.

Плотность вероятности при нормальном распределении случайной величины:

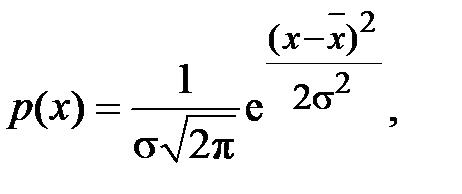
где 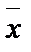– среднее значение случайной величины; σ² – дисперсия.

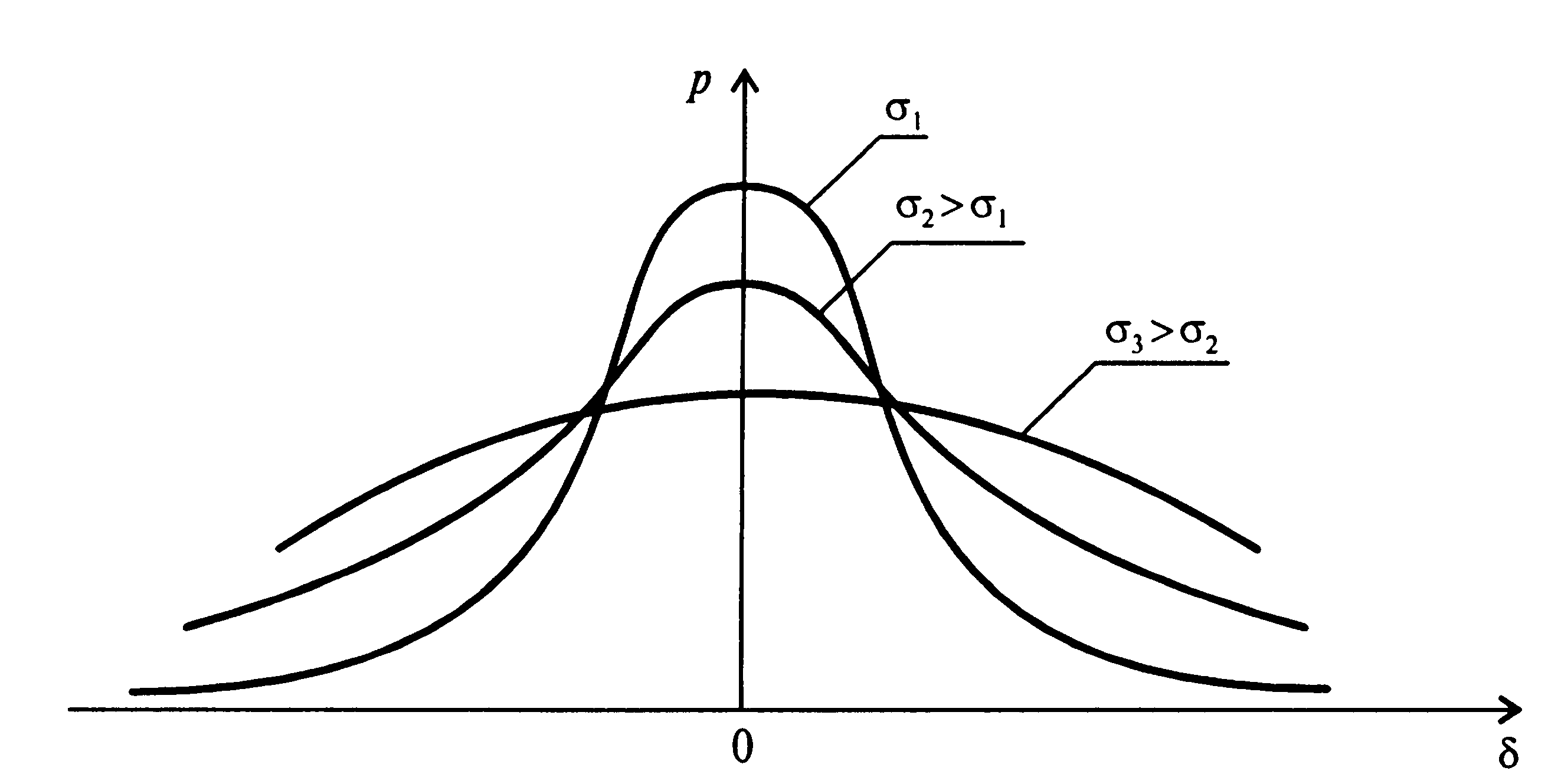
Рис. 1.5. Нормальное распределение погрешности измерения при

различных значениях σ

Оценками рассеяния результатов измерений относительно их среднего значения могут быть: размах, средняя квадратическая погрешность или стандартное отклонение (среднее квадратическое отклонение), доверительные границы погрешности (доверительная граница или доверительная погрешность).

1. Размах R_n – оценка рассеяния результатов единичных измерений физической величины, образующих ряд (или выборку из n измерений), вычисляемая по формуле

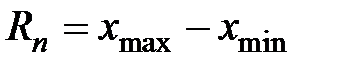, (1.18)

где x_max и x_min – наибольшее и наименьшее значения физической величины в данном ряду измерений.

2. Cредняя квадратическая погрешность результатов единичных измерений в ряду измерений (средняя квадратическая погрешность, СКП) – оценка рассеяния единичных результатов измерений в ряду равноточных измерений одной и той же физической величины около среднего их значения. Для нормального закона распределения СКП вычисляется по формуле:

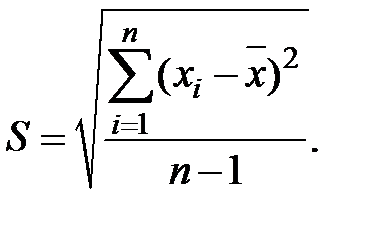(1.19)

где x_i – результат i-го единичного измерения; 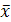– среднее арифметическое значение измеряемой величины из n единичных результатов.

При увеличении числа измерений значение S стремится к некоторому постоянному значению σ:

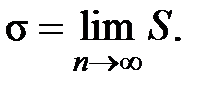
Квадрат σ и представляет собой дисперсию.

3. Для установления границ случайной погрешности используются доверительные границы погрешности результата измерений (доверительные границы погрешности) – наибольшее и наименьшее значения погрешности, ограничивающие интервал, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результата измерений.

В случае нормального закона распределения доверительные границы вычисляются как ±tS, где S – средняя квадратическая погрешность измерений; t – коэффициент, зависящий от доверительной вероятности р и числа измерений n. В общем случае t зависит и от формы закона распределения.

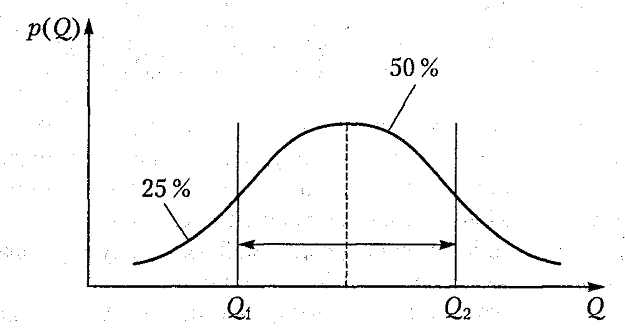
Рис. 1.6. Определение доверительных границ случайной

погрешности на основе квантилей

Площадь, заключенная под всей кривой плотности распределения вероятности, по условиям нормирования равна единице. Эту площадь можно разделить вертикальными линиями на части. Абсциссы Q таких линий называют квантилями (рис. 1.6).

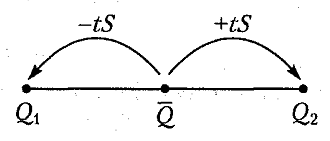
Здесь Q₁ есть 25 %-ная квантиль, так как площадь под кривой p(Q) слева от нее составляет 25 % всей площади. Абсцисса Q₂ соответствует 75 %-ной квантили. Между Q₁ и Q₂ заключено 50 % всех возможных значений случайной величины (результатов единичных измерений). Интервал, ограниченный значениями Q₁ и Q₂, называется доверительным интервалом, а соответствующая ему вероятность – доверительной вероятностью. Границы доверительного интервала указывают симметрично относительно среднего арифметического значения и устанавливают кратными СКП (рис. 1.7).

Рис. 1.7. Доверительный интервал

Доверительные границы случайной погрешности находят по формуле:

ε = ±tS. (1.21)

При интервальном оценивании случайной погрешности указывают значение принятой доверительной вероятности, например: U = (3,0 ± 0,2) В при р = 0,95.

В табл. 1.6 приведены доверительные вероятности при различных значениях t для нормального закона распределения при числе независимых наблюдений n > 50 (при n < 50 используются коэффициенты Стьюдента).

Таблица 1.6. Зависимость коэффициента t от доверительной вероятности Р для нормального закона распределения

При технических измерениях обычно принимается Р = 0,95 (правило 2S). Во многих случаях погрешность 3S принимают за предельную, в этом случае в доверительный интервал ±3S попадают 99,7 % погрешностей результатов измерений (Р = 0,997).

При суммировании нескольких независимых составляющих случайной погрешности суммируют их дисперсии (а не доверительные интервалы):

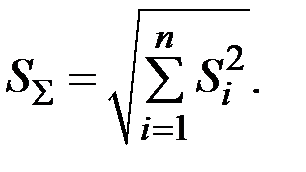
Форма закона распределения при суммировании случайных величин сохраняется лишь для небольшого числа законов распределения: нормального, закона Пуассона и некоторых других. Этим во многом объясняется значительная роль нормального закона распределения в метрологии. В общем случае при суммировании случайных величин законы их распределения деформируются и закон распределения суммы оказывается отличным от закона распределения слагаемых. Соответственно усложняется проблема определения доверительного интервала по отношению к конечному результату.