Случайные величины и их вероятностное описание
Случайной называют такую величину, которая в результате опыта может принять заранее неизвестное значение. Случайные величины, принимающие только отделенные друг от друга значения, которые можно заранее перечислить, называются дискретными. Такими величинами являются, например, возможное число очков при бросании кости, возможное число попаданий при ста выстрелах, возможное число горошин в одном килограмме. Величины, возможные значения которых не отделены друг от друга и непрерывно заполняют некоторый промежуток, называются непрерывнымислучайными величинами. Промежуток, который заполняют подобные величины, может иметь как резко выраженные границы, так и границы неопределенные, расплывчатые. Непрерывными случайными величинами являются длина отрезка линии, промежуток времени, интервал температуры и т. д.
Граница между дискретными и непрерывными величинами зачастую четко не определена. Некоторое количество воды в стакане может рассматриваться как величина непрерывная. Но вода состоит из отдельных молекул, и количества ее могут отличаться одно от другого на целое число молекул, то есть при возможности подсчета отдельных молекул количество воды можно было бы рассматривать как дискретную величину. Обычно при измерении принимают допущение о том, что измеряемые величины являются непрерывными.
Для полной характеристики дискретной случайной величины необходимо и достаточно знать все возможные ее значения и вероятность появления каждого из этих значений. Предположим, что при помощи цифрового омметра с дискретностью отсчета 1 Ом получены десять значений сопротивления цепи xk (k = 1,2,..., m), (табл. 1.4); nk (k = 1, 2,..., m) – количество реализаций каждого значения.
Таблица 1.4. Значения случайной величины с учетом повторяемости
| Значение хk, Ом | ||||||
| Число реализаций nk | ||||||
| Вероятность рk (Fk) | 0,1 | 0,3 | 0,2 | 0,3 | 0,1 |
На основе полученных данных может быть вычислено среднее арифметическое значение для дискретной случайной величины
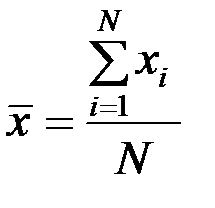 . (1.6)
. (1.6)
В другой форме записи оно будет выглядеть так:
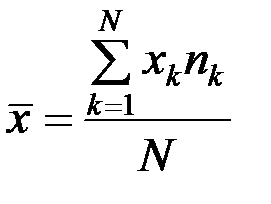 . (1.7)
. (1.7)
Вместо значения nk, показывающего, сколько раз было получено показание хk, вводят относительные частоты Fk = nk /N, которые при N→∞, стремятся к вероятностям рk появления конкретных значений дискретной случайной величины. Значения рk и Fk приведены в третьей строке табл. 1.4.
Законом распределения (законом распределения вероятности) случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Простейшей формой задания закона распределения является таблица, аналогичная табл. 1.5, которая часто называется рядом распределения случайной величины Х.
Таблица 1.5
| x | x1 | x2 | x3 | x4 | x5 | … |
| р | p1 | p2 | p3 | p4 | p5 | … |
При этом сумма вероятностей равна единице:
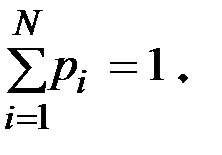 (1.8)
(1.8)
Считается, что если сумма набора чисел равна 1, то эти числа нормированы. Поэтому выражение (1.8) называется условием нормировки.
Ряд распределения может быть представлен в графическом виде. На графике по оси абсцисс откладывают возможные значения случайной величины, а по оси ординат – вероятности этих значений (рис. 1.2).
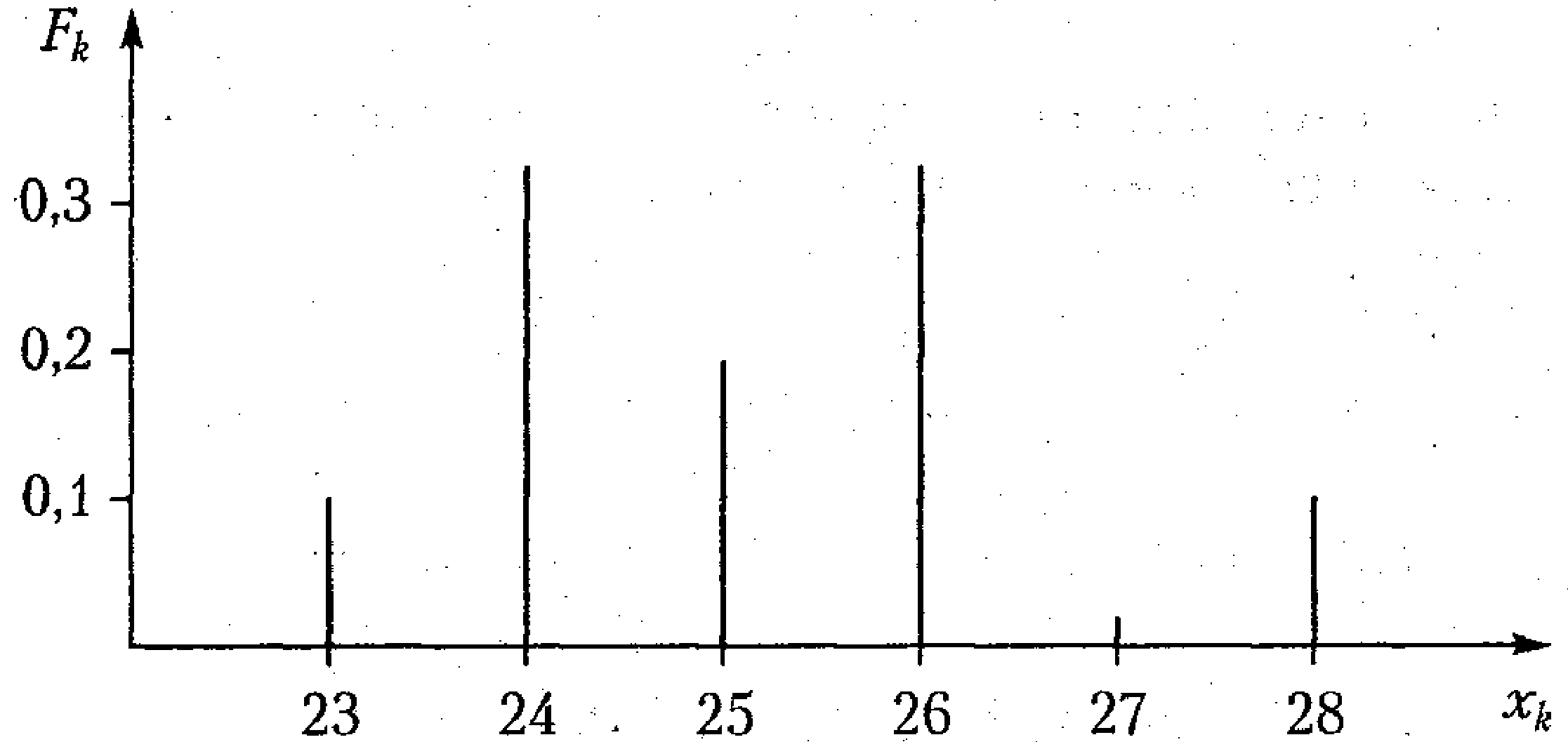
Рис. 1.2 График распределения дискретной случайной величины
Для описания дискретной случайной величины помимо закона распределения чаще всего используются такие числовые характеристики как математическое ожидание и дисперсия.
Математическое ожидание вычисляется как сумма произведений всех возможных ее значений на вероятность этих значений:
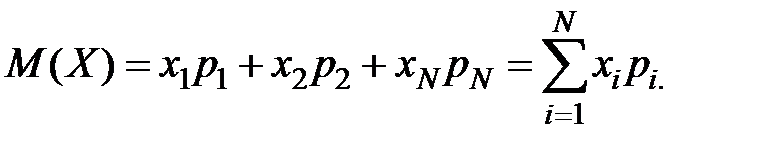 (1.9)
(1.9)
На практике при ограниченном числе наблюдений пользуются оценкой математического ожидания, которой является среднее арифметическое, вычисляемое согласно (1.7). Значения хk получаются в результате измерительного эксперимента.
Дисперсия является математическим ожиданием квадрата отклонения случайной величины от ее математического ожидания.
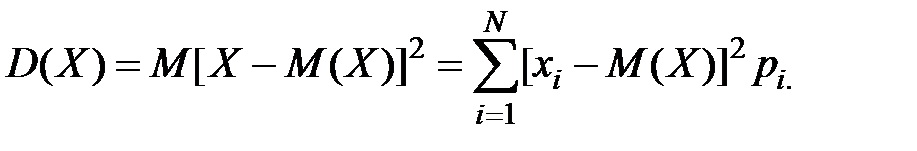 (1.10)
(1.10)
Как следует из (1.10), дисперсия имеет размерность квадрата случайной величины, поэтому вводят понятие среднего квадратического отклонения (CKO), под которым понимают квадратный корень из дисперсии. CKO σx имеет размерность самой случайной величины:
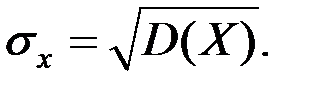 (1.11).
(1.11).
Дисперсия и СКО служат для оценки степени разброса случайной величины относительно ее среднего значения.
Непрерывная случайная величина имеет бесчисленное множество возможных значений, поэтому ее нельзя задать тем же законом распределения, что и дискретную случайную величину. Составить таблицу, в которой были бы перечислены все возможные значения непрерывной случайной величины, невозможно. Для количественной характеристики распределения вероятности в этом случае пользуются не вероятностью события X = х, а вероятностью события X < х, где х некоторая текущая переменная. Вероятность этого события зависит от х и является некоторой функцией от х. Эта функция называется функцией распределения вероятности случайной величины X и обозначается F(x):
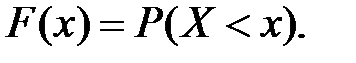 (1.12)
(1.12)
Функцию распределения F(x) иногда называют интегральной функцией распределения или интегральным законом распределения. Функция распределения вероятности является универсальной характеристикой и существует для всех случайных величин, как дискретных, так и непрерывных.
Некоторые общие свойства функции распределения можно сформулировать следующим образом:
1. Функция распределения F(x) есть неубывающая функция своего аргумента, то есть при х2 > хх F(x2) > F(xt).
2. При х = – ∞ F(– ∞) = 0, то есть на минус бесконечности функция распределения равна 0.
3. При х = +∞ F(+∞) = 1, то есть на плюс бесконечности функция распределения равна 1.
Для непрерывной случайной величины с непрерывной и дифференцируемой функцией распределения вероятности F(x) можно найти дифференциальный закон распределения вероятностей, выражаемый как
p(x) = Fʹ(x). (1.13)
Эта функция иначе называется плотностью распределения вероятности или дифференциальной функцией распределения. Она всегда неотрицательна и подчинена условию нормирования в виде
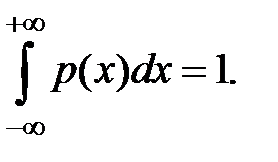 (1.14)
(1.14)
В измерительной практике часто используется равномерный закон, при котором возможные значения непрерывной случайной величины находятся в пределах некоторого конечного интервала, причем в пределах этого интервала все значения случайной величины обладают одной и той же плотностью вероятности (рис. 1.3).
Аналитически равномерное распределение случайной величины записывается в виде
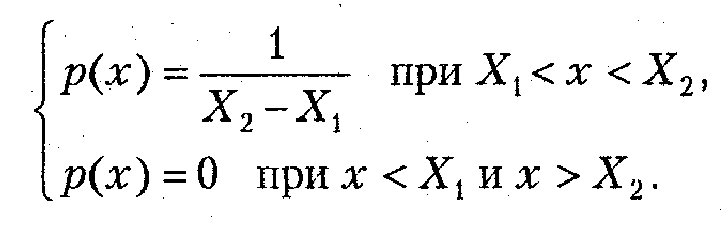
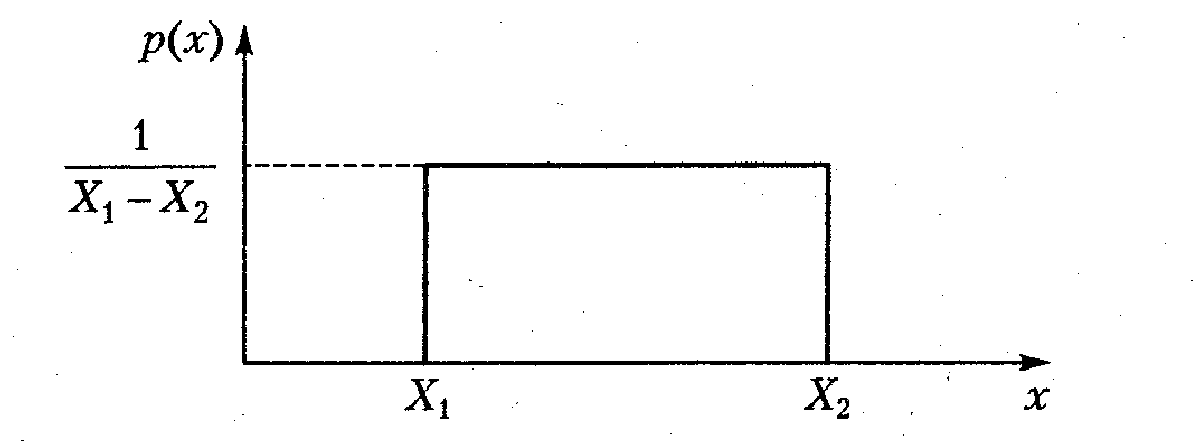
Рис. 1.3. Равномерный закон плотности вероятности
Другим законом, который имеет большое значение в метрологической практике, является нормальный закон распределения случайной величины.
Плотность вероятности при нормальном распределении случайной величины:
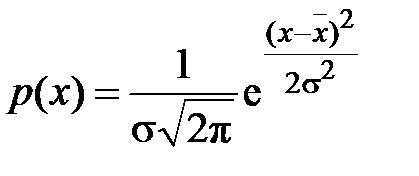 , (1.16)
, (1.16)
где х – среднее значение; σ – среднее квадратическое отклонение.
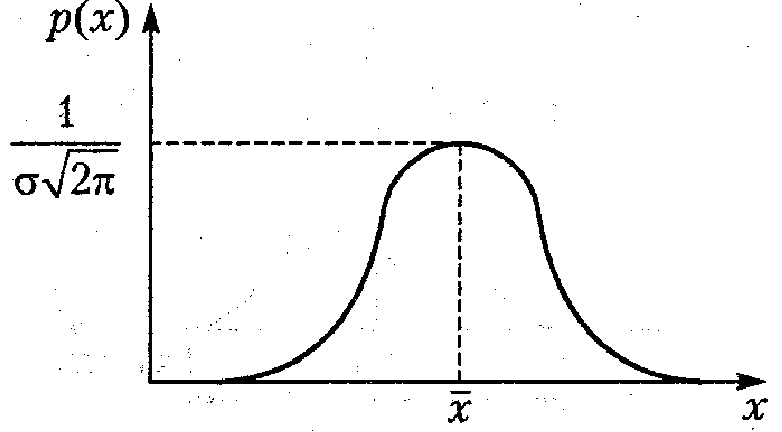
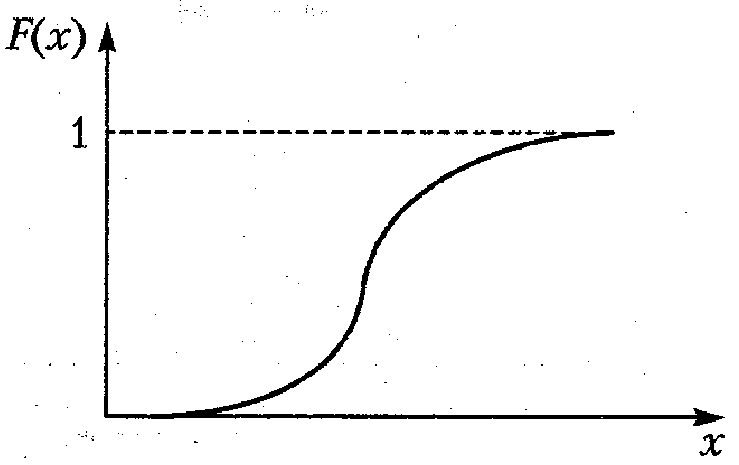
Общий вид дифференциальной р(х) и интегральной F(x) функций распределения для нормального закона приведен на рис. 1.4.
а б
Рис. 1.4. Дифференциальная (а) и интегральная (б) функции
распределения для нормального закона
Дата добавления: 2016-02-13; просмотров: 2132;
