Формула сложения вероятностей.
Пусть события А и В совместны, т.е. 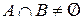 . Тогда
. Тогда
 ,. (1)
,. (1)
т.е. вероятность объединения двух совместных событий равна сумме их вероятностей без вероятности их пересечения.
Замечание. 1. Формула (1) справедлива для любых событий А и В, т.к. если события А и В несовместны, т.е. 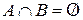 , то
, то  . В результате формула (1) переходит в аксиому сложения Р3 для двух событий.
. В результате формула (1) переходит в аксиому сложения Р3 для двух событий.
Замечание. 2. Формула (1) называется теоремой (формулой) сложения вероятностей.
Можно получить формулу сложения вероятностей для трех и большего числа совместных событий. Так для трех событий она имеет вид
 . (2)
. (2)
Для п событий:
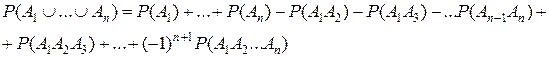 (3)
(3)
Замечание 3. Иногда проще найти вероятность объединения нескольких событий 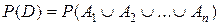 , используя равенство
, используя равенство  , где
, где 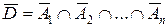 противоположно событию D. Тогда
противоположно событию D. Тогда 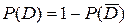 .
.
Пример. Бросаются две игральные кости. Какова вероятность появления хотя бы одной шестерки?
Решение. А = {появление шестерки на первой кости}
В= {появление шестерки на второй кости}
АÈВ= {появление хотя бы одной шестерки при бросании костей}
События А и В совместные. По формуле (1) находим 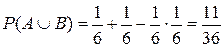 .
.
Иначе:  . Следовательно,
. Следовательно, 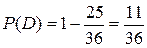 .
.
Дата добавления: 2016-03-04; просмотров: 1194;
