Нормы векторов и матриц

Для исследования сходимости и точности численных итерационных методов решения задач линейной и нелинейной и нелинейной алгебры, в том числе итерационных методов решения СЛАУ и СНАУ, необходимо ввести понятие нормы векторов матриц.

Нормой вектора х = 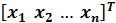(обозначают )

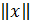В n - мерной вещественном пространстве векторов x 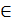Rⁿ называют неотрицательное число, вычисляемое с помощью компонент вектора и обладающее следующими свойствами

а) 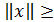0 ( = 0 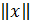тогда и только тогда, когда x – нулевой вектор, т.е. x = );

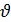б) 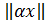= 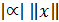для любых чисел 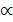(действительных или комплексных);

в) .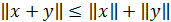

Нормой матрицы А_n+n(обозначается 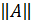c вещественными элементами в n-мерном пространстве матриц А 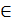Rⁿназывают неотрицательное число, вычисляемое с помощью элементов матрицы и обладающее следующими свойствами:

а) 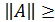0 ( 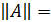0 тогда и только тогда, когда А – нулевая матрица, т.е. А= );

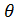б) 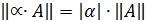для любых действительных и комплексных чисел ;

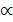в) + ;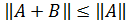

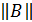г) 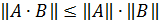для всех 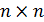матриц А и 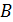рассматриваемого пространства.

Нормы матриц и векторов, на которые матрицы действуют должны быть согласованы.

Норма матрицы А называется согласованной с нормой вектора х, на который действует матрица А; если выполняется неравенство

∙ , (*)

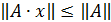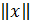которое называется связью, осуществляющей согласование матрицы А с вектором х.

Наиболее употребительными являются следующие нормы векторов:

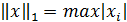, I = , …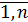

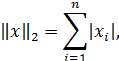
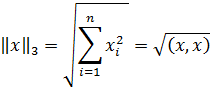
Согласованными с ними с помощью связи нормами матриц будут соответственно:

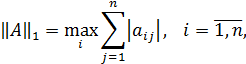
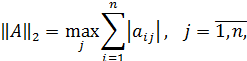
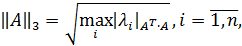
Где 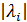- модули собственных чисел симметрической вещественной матрицы 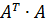для которой все 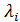являются действительными числами;

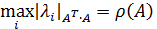- максимальное по модулю собственное значение матрицы 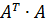или спектральный радиус вещественной матрицы А.

Основная и дополнительная литература по дисциплине.

Основная:

1. Формалев В.Ф., Ревизников Д.Л. Численные методы.-М.: Физматлит 2004-400с.

2. Пирумов У.Г. (редактор). Численные методы. Учебник и практикум. Бакалавр. Академический курс.-М.: Юрайт, 2014-422с.

3. Численные методы. Сборник задач. Под редакцией У.Г.Пирумова.-М.: Дрофа, 2007-144с.

Дополнительная:

4. Вержбицкий В.М. Численные методы. Три книги:

1) Линейная алгебра и нелинейные уравнения.

2) Математический анализ и ЛДУ.

3) Дифференциальные уравнения в частных производных.

5. Демидович Б.П., Марон И.А. Основы вычислительной математики.-М.: наука, 1966, - 664с.

Учебная литература к лекции 1:

, с.3…15; ,с.3…6.