Источники погрешностей

Предмет изучения в дисциплине и структура дисциплины.

Предметом изученияв дисциплине являются численные методы по четырем направлениям.

Численные методы – это методы решения задач, сводящиеся к арифметическим и логическим действиям над числами, то есть к действиям, которые выполняют ЭВМ.

В данной дисциплине численные методы изучаются по следующим направлениям: численные методы алгебры; численные методы приближения, дифференцирования и интегрирования функций; численные методы решения задачи Коши и краевой задачи для обыкновенных дифференциальных уравнений (ОДУ); численные методы оптимального оценивания параметров.

Различаются прямые и итерационные численные методы. Прямыечисленные методы – это такие методы, которые дают решение задачи за конечное, точно определяемое для каждого метода, число операций. Итерационные численные методы – Это такие методы, которые дают решение задачи как предел бесконечной последовательности приближенныхрешений, в которых каждое последующее более точное приближение находится по уже найденному предыдущему.

Трудоемкость дисциплины 2 зачетные единицы. Одна зачетная единица соответствует 36 академическим часам. Академический час соответствует 45 минутам. На изучение дисциплины с преподавателем отводится 48 академических часов и на самостоятельную работу курсантов отводится 24 академических часов. Для обучения курсантов дисциплине используются три образовательные технологии – лекции, лабораторные работы и практические занятия. Учебной программой дисциплины предусмотрено 12 лекций (24 часа), 4 лабораторных занятия (16 часов) и 3 практических занятия (6 часов). Отчетность по дисциплине изучается в 4-м семестре.

Структура дисциплинывключает: введение в дисциплине(лекция);

тему1. Численные методы алгебры(3 лекции, 2 лабораторные работы); тему 2. Приближение функций. Численное интегрирование и дифференцирование (3 лекции, 3 практических занятия); тему 3. Численные методы решения обыкновенных дифференциальных уравнений(2 лекции, 2 лабораторные работы); тема 4. Численные методы оптимальных оценок параметров (3 лекции); заключение по дисциплине (лекция 12, третий вопрос).

Источники и исчисление погрешностей

Источники погрешностей

Существует четыре источника погрешностей в результате, полученном численным методом:

1. Математическая и физическая модель задачи.

2. Исходные данные.

3. Приближенность (погрешность) метода.

4. Округление результата.

Первые два источника погрешностей приводят к так называемой неустранимой погрешности. Эта погрешность может присутствовать, даже если решение сформулированной задачи найдено точно.

Погрешность метода возникает из-за того, что 1) точный оператор и исходные данные, в частности начальные и краевые условия, заменяются по определенным правилам приближенными. Так, производные заменяются их разностными аналогами, интегралы – суммами, функции – специальными многочленами; 2) при решении многих задач строятся бесконечные итерационные процессы, которые естественным образом прекращаются после конечного числа операций. Как правило,погрешность метода может быть оценена и поддается контролю. При изучении численных методов такая оценка будет сделана. Погрешность метода следует выбирать так, чтобы она была на порядок меньше неустранимой погрешности.

Погрешность округления возникает в связи с тем, что вычисления производятся с конечным числом значащих цифр. Округления производятся по следующему правилу: если в старшем из отбрасываемых разрядов стоит цифра меньше 5, то содержимоесохраняемых разрядовне изменяется. В противном случае в младший сохраняемый разряд добавляется единица с тем же знаком, что и у самого числа. Очевидно, что погрешность, возникающая при округлении, не превышает единицы младшего оставляемого (сохраняемого) разряда. Поскольку на современных ЭВМ число записывается, как правило, минимум с 10…12 десятичными знаками после запятой, то погрешность единичного округления 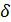= 10^-10… 10^-12 обычно пренебрежима мала по сравнению с неустранимой погрешностью и погрешностью метода. При решении больших задач производятся миллиарды операций и можно предположить, что ошибки могут заметно накапливаться, однако, поскольку они носят случайный характер, может происходить их взаимная компенсация. Зачастую строятся специальные алгоритмы, в частности итерационные, которые малочувствительны к ошибкам округления.