УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ.
Теорема 1.Произвольную систему сил при помощи элементарных операций можно преобразовать в эквивалентную систему, состоящую из двух сил; при этом главный вектор и главный момент системы не изменятся.
Доказательство. Докажем эту теорему для системы, состоящей из трех сил.Пусть к твердому телу в точках А, В и С приложены силы 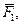
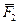 и
и 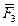 (рис.27).
(рис.27).
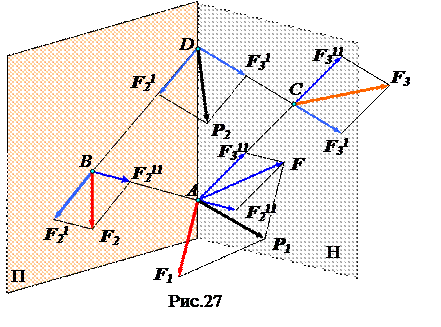
Будем считать, что эти силы не лежат в одной плоскости. Проведем через точку А и силу 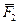 плоскость П, а через точку А и силу
плоскость П, а через точку А и силу 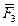 - плоскость Н. Выберем на линии пересечения этих плоскостей произвольную точку D. Соединим точки А и D с точками В и С. Разложим силу
- плоскость Н. Выберем на линии пересечения этих плоскостей произвольную точку D. Соединим точки А и D с точками В и С. Разложим силу 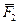 на две составляющие
на две составляющие 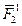 и
и 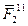 , направленные по прямым АВ и ВD и перенесем эти составляющие по линиям их действия в точки А и D.
, направленные по прямым АВ и ВD и перенесем эти составляющие по линиям их действия в точки А и D.
Разложим силу 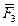 на составляющие
на составляющие 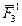 и
и 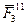 , направленные по прямым DС и AС, и перенесем эти составляющие вдоль их линий действия в точки А и D. Силы
, направленные по прямым DС и AС, и перенесем эти составляющие вдоль их линий действия в точки А и D. Силы 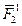 и
и 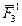 , приложенные в точке D, заменим, используя правило параллелограмма, одной силой
, приложенные в точке D, заменим, используя правило параллелограмма, одной силой 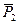 , приложенной в той же точке. Силы
, приложенной в той же точке. Силы 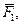
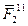 и
и 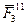 , приложенные в точке А, заменим, используя дважды правило параллелограмма, одной силой
, приложенные в точке А, заменим, используя дважды правило параллелограмма, одной силой 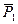 . Таким образом, исходная система сил
. Таким образом, исходная система сил 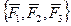 оказалась замененной системой
оказалась замененной системой 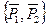 . Так как при этом применялись только элементарные операции, то системы
. Так как при этом применялись только элементарные операции, то системы 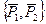 и
и 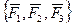 оказались эквивалентными, и, следовательно, их главные векторы и главные моменты не изменились:
оказались эквивалентными, и, следовательно, их главные векторы и главные моменты не изменились: 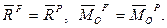
Если плоскости П и Н сливаются, то точку D можно брать где угодно в этих плоскостях.
Теорема доказана для системы, состоящей из трех сил. Если система состоит из большего числа сил, то, повторяя эту операцию несколько раз, приведем к двум силам и любую заданную систему сил.
Операция замены системы сил эквивалентной системой, состоящей из двух сил, называется приведением данной системы сил к двум силам.
Теорема 2 (о равновесии системы сил). Для равновесия произвольной системы сил необходимо и достаточно, чтобы главный вектор и главный момент относительно любого центра равнялись нулю.
Доказательство необходимости. Пусть система сил 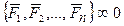 .
.
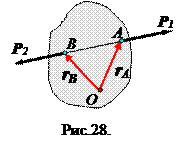 Докажем, что главный вектор системы равен нулю и главный момент относительно любого центра также равен нулю:
Докажем, что главный вектор системы равен нулю и главный момент относительно любого центра также равен нулю: 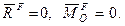
Заменим эту систему эквивалентной системой двух сил 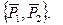
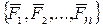 ¥
¥ 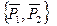 ¥ 0.
¥ 0.
| |
Если система 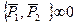 , то на основании первой аксиомы заключаем, что силы
, то на основании первой аксиомы заключаем, что силы 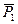 и
и 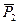 равны по модулю и направлены по одной прямой в противоположные стороны (рис.28). Главный вектор
равны по модулю и направлены по одной прямой в противоположные стороны (рис.28). Главный вектор 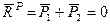 .
.
Главный момент системы 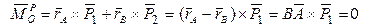 , так как векторы
, так как векторы 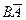 и
и 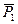 направлены по одной прямой.
направлены по одной прямой.
Следовательно, будут равны нулю главный вектор и главный момент системы 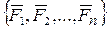 , т.е.
, т.е. 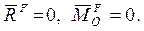
Доказательство достаточности. Пусть главный вектор и главный момент системы 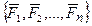 равны нулю:
равны нулю: 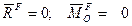 . (рис.28).
. (рис.28).
Докажем, что система находится в равновесии: 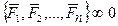 .
.
Заменим систему 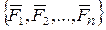 эквивалентной системой двух сил:
эквивалентной системой двух сил: 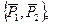 Тогда,
Тогда, 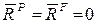 .
. 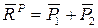 = 0.
= 0.
Следовательно, 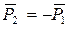
Определим главный момент системы 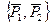 относительно точки О:
относительно точки О:
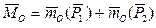 =
= 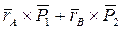 =0,
=0,
где 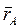 и
и 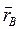 - радиусы-векторы, проведенные из точки О в точки приложения сил
- радиусы-векторы, проведенные из точки О в точки приложения сил 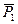 и
и 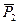 .
.
Заменим: 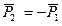 , получим:
, получим:
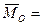
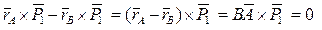 .
.
Векторное произведение равно нулю в том случае, когда один из сомножителей равен нулю, или когда перемножаемые векторы параллельны. В нашем случае 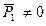 ,
, 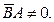 Следовательно, векторы
Следовательно, векторы 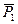 и
и 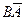 параллельны. Отсюда следует, что линии действия сил
параллельны. Отсюда следует, что линии действия сил 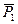 и
и 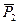 совпадают с прямой АВ.
совпадают с прямой АВ.
Итак, силы 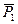 и
и 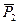 равны по модулю, и направлены по одной прямой в противоположные стороны, такие силы уравновешиваются, т.е.
равны по модулю, и направлены по одной прямой в противоположные стороны, такие силы уравновешиваются, т.е. 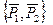 ¥0. Следовательно, эквивалентная ей система
¥0. Следовательно, эквивалентная ей система 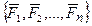 также находится в равновесии:
также находится в равновесии: 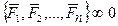 .
.
Дата добавления: 2016-02-13; просмотров: 723;
