ПОНЯТИЕ ЦЕНТРА ТЯЖЕСТИ.

На каждую частицу тела, находящегося вблизи поверхности Земли, действует сила притяжения, называемая силой тяжести. Все эти силы, строго говоря, направлены к центру Земли, но так как размеры тела невелики по сравнению с радиусом Земли, то направления этих сил практически будут параллельны и направлены вертикально вниз.

Силой тяжести тела называется равнодействующая всех сил тяжести, действующих на частицы тела. Обозначим 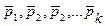силы тяжести, приложенные к частицам тела, их равнодействующую обозначим .

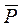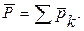
Центром тяжести тела называется точка С приложения силы тяжести тела.

При любом повороте тела силы 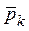остаются приложенными в одних и тех же точках и параллельными друг другу, но изменяется их направление относительно тела. Неизменным остается также положение центра тяжести относительно тела.

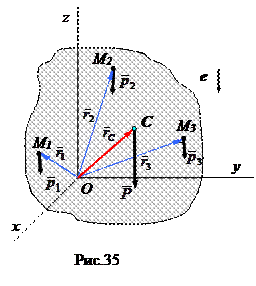
Определим положение центра тяжести тела относительно произвольно выбранной точки О. Соединим (рис.35) радиусами -векторами с точкой О точки приложения сил тяжести всех частиц и центр тяжести тела. Запишем теорему Вариньона:

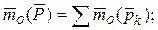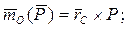
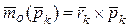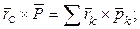так как , то или

Выберем единичный вектор 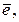определяющий направление сил тяжести. Тогда :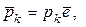 Подставим эти значения в предыдущее равенство: В этом выражении Р и р_k являются скалярными коэффициентами, поэтому их можно поставить перед векторами и , вектор 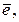можно вынести за скобки, получим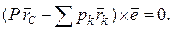

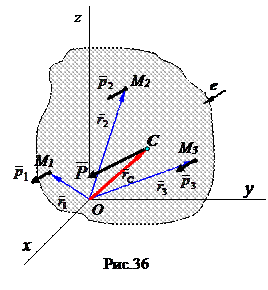
Как было отмечено выше, при повороте тела силы тяжести поворачиваются относительно него на один и тот же угол, а центр тяжести С сохраняет положение неизменным. Эту же ситуацию можно смоделировать (рис.36), повернув все силы тяжести на один и тот же угол вокруг точек приложения, оставив при этом тело неподвижным. Тогда единичный вектор изменит свое направление, и поэтому в общем случае он не будет параллелен вектору 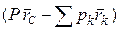. Так как вектор не равен нулю, то векторное произведение векторов 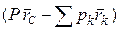и будет равно нулю только тогда, когда вектор 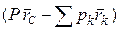будет равен нулю: 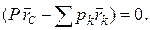Отсюда определяем значение радиуса - вектора 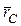центра тяжести тела.

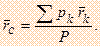
Свяжем с точкой С систему координат xyz . Тогда координаты цента тяжести в этом системе координат определяются следующими формулами:

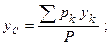
где 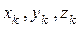- координаты точек приложения сил тяжести 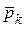, действующих на частицы тела.

Для однородного тела сила тяжести 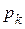любой его части пропорциональна объему v_k этой части: p_k=g v_k, а сила тяжести тела Р пропорциональна объему V этого тела: P=g V.

Подставив значения Р и р_к в формулы координат центра тяжести, получим:

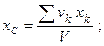
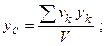
Положение центра тяжести тела, как следует из полученных формул, зависит только от геометрической формы тела, поэтому точку С называют центром тяжести объема.

Аналогично определим центр тяжести однородной плоской пластины, расположенной в плоскости ху:

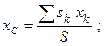
где S – площадь всей пластины, s_k – площади ее частей.

Точно также получаются координаты центра тяжести однороднойлинии:

,

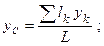
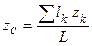где L – длина всей линии, l_k – длины ее частей.

Если однородное тела имеет плоскость, ось или центр симметрии, то его центр тяжести лежит в плоскости, на оси или в центре симметрии. Отсюда следует, что центр тяжести однородного стержня лежит в его середине, центр тяжести круглого кольца, круглой или прямоугольной пластины, шара находится в соответствующем геометрическом центре. Центры тяжести ромба, параллелограмма лежат в точках пересечения их диагоналей.

Для определения центра тяжести тело разбивается на конечное число частей, положение центра тяжести каждой из которых известно. Координаты центра тяжести тела вычисляются по общим формулам. В тех случаях, когда данное тела имеет отверстия, его можно представить как разность тел, в этом случае сила тяжести большего тела считается положительной величиной, а сила тяжести меньшего – отрицательной.

Если тело нельзя разбить на несколько конечных частей, положения центров тяжести которых известны, то тело разбивают на бесконечно большое элементарных частиц и положение центра тяжести тела определяется интегрированием. В этом случае координаты центра тяжести однородного твердого тела равны:

, ,

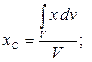
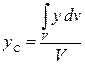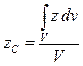где V – объем всего тела.

В случае однородной плоской фигуры, расположенной в плоскости ху:

,

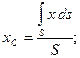
где S – площадь всей фигуры.

Для однородной линии, длина которой равна L, координаты центра тяжести равны: