Равновесие сходящейся системы сил.
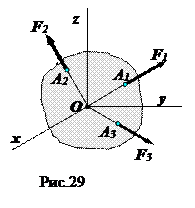Система сил называется сходящейся, если линии действия всех сил проходят через одну точку (рис.29).
Для равновесия сходящейся системы сил необходимо и достаточно, чтобы суммы проекций всех сил системы на выбранные координатные оси равнялись нулю.
для плоской сходящейся системы сил: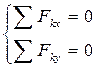 
1.5. МОМЕНТЫ СИЛ И ЗАВИСИМОСТИ МЕЖДУ НИМИ.
Моменты сил являются мерой вращательного действия сил на тело.
1.5.1. Вектором момента силы 
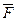
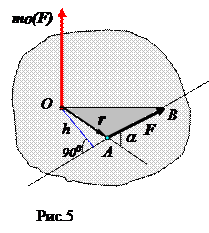
относительно центра О называется вектор mO( 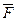), приложенный в этом центре, направленный перпендикулярно плоскости, в которой лежат центр и сила, в ту сторону, откуда поворот силы вокруг центра виден против часовой стрелки, и равный по модулю произведению модуля силы на плечо (рис.5).
Плечом силы относительно центра называется кратчайшее расстояние h между центром O и линией действия силы F.
Следовательно, модуль вектора-момента силы равен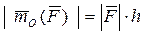 
. (Нм или Кн.м)
Так как h является высотой треугольника ОАВ, то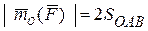 
, где SОАВ - площадь треугольника ОАВ.
Вектор момента силы относительно центра равен векторному произведению радиуса-вектора, проведенного из центра в точку приложения силы, и вектора силы, так как эти два вектора имеют одинаковые модули и направления.
.
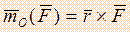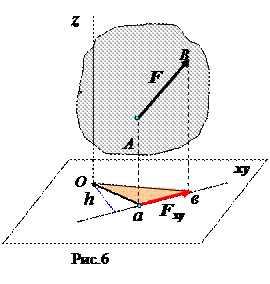
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную этой оси, относительно точки пересечения оси с плоскостью (рис.6).
Момент силы относительно оси считается положительным, если проекция силы на плоскость, перпендикулярную оси, стремится повернуть тело вокруг положительного направления оси против часовой стрелки, отрицательным, если – по часовой стрелке. Момент силы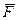 
относительно оси z обозначается символом 
. 
= 
,
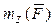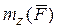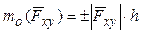где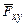 
– проекция силы 
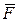на плоскость xy, перпендикулярную оси z.
Так как h является высотой треугольника Оав, то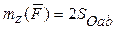 
,
где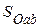 
– площадь треугольника Оав.
Для определения момента силы 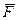относительно оси z нужно выполнить следующие действия:
1. провести плоскость xy, перпендикулярную оси z и указать точку О пересечения оси z с этой плоскостью;
2. найти проекцию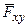 
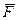силы на плоскость xy;
3. из точки О опустить перпендикуляр h на линию действия проекции 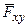и вычислить момент 
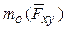как произведение модуля проекции силы 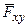на плечо h с соответствующим знаком.
Момент силы относительно оси равен нулю, если сила параллельна оси или пересекает ось, т.е. в том случае, когда ось и действующая сила лежат в одной плоскости.
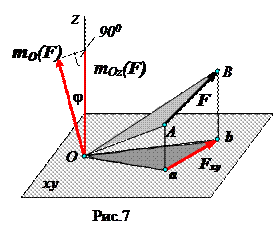Теорема 1. Проекция векторного момента силы относительно центра на ось, проходящую через этот центр, равна моменту силы относительно этой оси.
Доказательство. Проведем через 
точку О ось z и спроецируем на нее вектор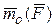 
(рис.7):
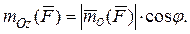
Модуль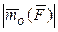 
равен удвоенной площади треугольника ОАВ: 
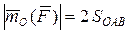. Cледовательно,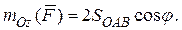 
Момент силы 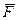относительно оси z 
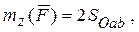где треугольник Оав является проекцией треугольника ОАВ на плоскость, перпендикулярную оси z. Значит, 
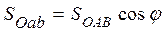, где j угол между плоскостями этих треугольников, измеряемый углом между перпендикулярами к ним.
Окончательно,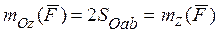 
.
Следовательно,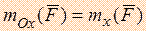 
,
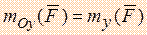
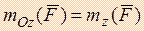
Выражение момента силы относительно оси в координатной форме.
Разложим векторный момент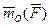 
силы 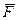относительно центра О по координатным осям x, y, z, связанным с центром О.
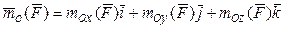
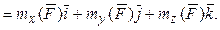(1)
Разложим также по координатным осям векторное произведение.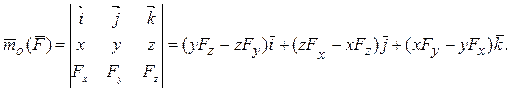 
(2)
Исходные данные: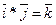 
, 
, 
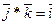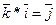
Сравнивая (1) и (2), получаем выражения моментов силы 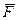относительно координатных осей.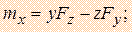 
,
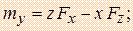
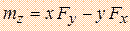где x, y, z - координаты точки приложения силы, а Fx, Fy, Fz - проекции силы
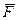на оси координат.
1. 5.2. Моменты для плоской системы сил
Дата добавления: 2016-02-13; просмотров: 1096;