Связями называются любые ограничения, препятствующие перемещениям тела в пространстве.
К связям относятся различного вида устройства, закрепляющие тела, и опорные поверхности.
Тело с наложенными на него связями называется несвободным.
Реакцией связи называется сила, с которой связь действует на тело.
Направления реакций определяются свойствами связей. Реакция конкретной связи направлена в сторону, противоположную той, куда эта связь не дает телу перемещаться.
Все силы, действующие на несвободное тело, разделяются на две категории: активные силы и реакции связей. Силы, не зависящие от связей, называются активными или заданными. Реакции связей являются пассивными, поскольку они возникают в результате действия на тело активных сил.
1.5. Статика решает две задачи:
1) определяет методы эквивалентных преобразований систем сил;
2) определяет условия равновесия абсолютно твердых тел.
Равновесием в статике называется состояние покоя данного тела или нескольких тел по отношению к инерциальной системе отсчета.
Для инженерных расчетов инерциальной системой может служить система координат, связанная с Землей.
АКСИОМЫ СТАТИКИ.
Аксиома 1. Для равновесия абсолютно твердого тела под действием двух приложенных к нему сил необходимо и достаточно, чтобы силы были равны по модулю и направлены по одной прямой в противоположные стороны (рис.13).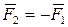 
.
Аксиома 2. Действие данной системы сил на абсолютно твердое тела не изменится, если добавить к ней или отнять от нее уравновешенную систему сил.
Если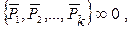 
то 
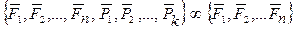
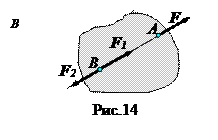
Следствие. Действие силы на абсолютно твердое тело не изменится, если перенести силу вдоль линии действия в любую точку тела (рис.14).
Доказательство. Пусть сила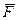 
приложена в точке А. Приложим в точке В, находящейся на линии действия этой силы, две равные по модулю и противоположные по направлению силы 
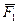и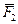 
Выберем 
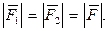По аксиоме 1 система сил 
.
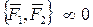На основании аксиомы 2 имеем:
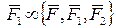(1)
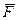Силы и 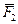также удовлетворяют аксиоме 2, следовательно, 
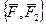¥ 0.
Тогда 
¥ 
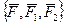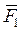.(2)
Сравнивая (1) и (2), получаем: ¥ .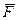
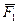Аксиома 3. Две силы, приложенные в одной точке, имеют равнодействующую, приложенную в той же точке и определяемую диагональю параллелограмма, построенного на этих силах как на сторонах.
Вектор 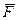, равный диагонали параллелограмма, построенного на векторах 
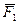и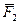 
(рис. 15) называется геометрической суммой этих векторов.
= +
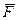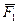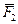
Аксиома 4. При всяком действии одного тела на другое силы их взаимодействия равны по модулю и направлены по одной прямой в противоположные стороны. Указанные силы приложены к разным телам, поэтому вместе они не составляют уравновешенную систему сил.
Аксиома 5. Равновесие деформируемого тела, находящееся под действием системы сил не нарушится, если тело считать абсолютно твердым.
Дата добавления: 2016-02-13; просмотров: 1772;