Закон Джоуля - Ленца в дифференциальной форме
Согласно закону Джоуля - Ленца (28) в элементарном цилиндрическом объеме dV с площадью поперечного сечения dS и длиной dl за время dt выделится тепло
dQ =I  Rdt =(jdS)
Rdt =(jdS) 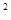
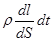 =
= 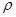 j
j 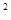 dldSdt =
dldSdt = 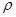 j
j 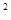 dVdt.
dVdt.
Разделив на dV и dt, найдем количество тепла, выделяющееся в единицу времени в единице объема Q 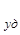 =
= 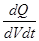 =
= 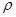 j
j 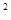 . (37)
. (37)
здесь Q 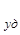 -называется удельной тепловой мощностью тока, которая в СИ измеряется в Вт/м3.
-называется удельной тепловой мощностью тока, которая в СИ измеряется в Вт/м3.
С учетом (16) из (37) следует, что Q 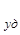 =
= 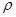 j
j 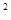 =
= 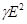 . (38)
. (38)
Формулы (37) и (38) выражают закон Джоуля - Ленца в дифференциальной форме.
Правила Кирхгофа
      I1
I2 I3
Рис. 6 I1
I2 I3
Рис. 6
| В основе расчета электрических цепей лежат два правила Кирхгофа: 1) АЛГЕБРАИЧЕСКАЯ СУММА ТОКОВ, СХОДЯЩИХСЯ В УЗЛЕ, РАВНА НУЛЮ, т. е. 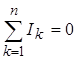 . (39) . (39)
|
Току, текущему к узлу, приписывается один знак ("+" или "-"), а току, текущему от узла, - другой знак; таким образом, для направлений токов в узле электрической схемы, пред- ставленном на рис. 6, имеем  .
.
2) В ЛЮБОМ ЗАМКНУТОМ КОНТУРЕ АЛГЕБРАИЧЕСКАЯ СУММА НАПРЯЖЕНИЙ НА ВСЕХ УЧАСТКАХ ЭТОГО КОНТУРА РАВНА АЛГЕБРАИЧЕСКОЙ СУММЕ ЭДС, ВСТРЕЧАЮЩИХСЯ В ЭТОМ КОНТУРЕ 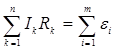 (40)
(40)
 При этом также следует придерживаться правила знаков: токи, текущие вдоль выбранного направления обхода контура считаются положительными, а идущие против направления обхода - отрицательными. Соответственно положительными считаются ЭДС тех источников, которые вызывают ток, совпадающий по направлению с обходом контура (см. рис.7), где обозначает направление обхода контура .
При этом также следует придерживаться правила знаков: токи, текущие вдоль выбранного направления обхода контура считаются положительными, а идущие против направления обхода - отрицательными. Соответственно положительными считаются ЭДС тех источников, которые вызывают ток, совпадающий по направлению с обходом контура (см. рис.7), где обозначает направление обхода контура .

| |
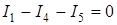 ,
,
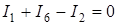 ,
,
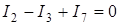 ,
,
 .
.
Дата добавления: 2016-03-04; просмотров: 848;
