Энергия заряженного проводника, системы проводников и конденсатора

Пусть проводник имеет емкость С, заряд q, потенциал 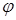; тогда работа, совершаемая против сил электрического поля при перенесении заряда 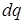из бесконечности на проводник, будет 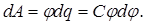(11)

Чтобы зарядить проводник от нуля до потенциала 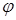, необходимо совершить работу

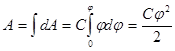. (12)

Энергия заряженного проводника ,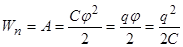

полная энергия системы заряженных проводников 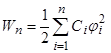. (13)

Для конденсатора 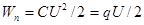. (14)

Энергия электрического поля. Объемная плотность энергии электрического поля в диэлектрике и в вакууме

Покажем, что формула (14) выражает энергию электрического поля. Подставляя в (14) выражение для емкости плоского конденсатора (8) и учитывая, что U = Ed, находим

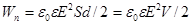, (15)

где V - объем, занятый электрическим полем. Объемная плотность энергии

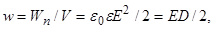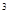Дж/м (16)

Из (16) следует, что объемная плотность энергии электрического поля в вакууме ( 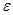=1)

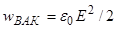. (17)

С учетом этого объемная плотность энергии поляризованного диэлектрика

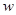
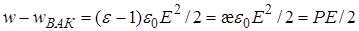= , (18)

где 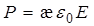- поляризованность диэлектрика, 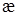– его диэлектрическая восприимчивость; 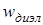– характеризует энергию, которая была затрачена при поляризации диэлектрика.