Электрическая емкость
Будем сообщать уединенному проводнику разные по величине заряды 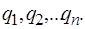 При этом проводник будет иметь разные по величине потенциалы
При этом проводник будет иметь разные по величине потенциалы 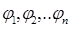 .Оказывается отношение
.Оказывается отношение 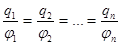 - есть величина постоянная для данного проводника и не зависит от величины сообщенного заряда, а зависит только от геометрической формы проводника и диэлектрической проницаемости окружающей его среды.
- есть величина постоянная для данного проводника и не зависит от величины сообщенного заряда, а зависит только от геометрической формы проводника и диэлектрической проницаемости окружающей его среды.
Это отношение дает величину электроемкости уединенного проводника, т.е.
C=q/ 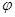 . (5)
. (5)
Электрическая емкость измеряется в фарадах: 1Ф= 1Кл / 1В, а также в мФ, мкФ, нФ, пФ ...; причем 1мФ = 10-3 Ф, 1мкФ = 10 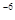 Ф, 1 нФ =
Ф, 1 нФ = 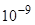 Ф, 1 пФ =
Ф, 1 пФ = 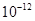 Ф.
Ф.
Потенциал заряженного шара радиуса R равен 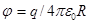 , с учетом этого находим емкость уединненого шарового проводника:
, с учетом этого находим емкость уединненого шарового проводника: 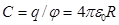 , (6)
, (6)
т.е. оказывается , что С пропорциональна радиусу шарового проводника R.
Подсчитаем емкость Земного шара, имеющего радиус 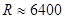 км
км 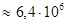 м.
м.
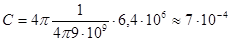 Ф = 700 мкФ.
Ф = 700 мкФ.
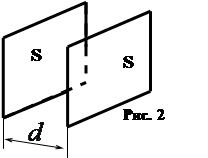 Для получения большей емкости используют конденсаторы в виде двух проводников, помещенных близко друг от друга. В этом случае емкость
Для получения большей емкости используют конденсаторы в виде двух проводников, помещенных близко друг от друга. В этом случае емкость 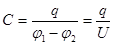 . (7)
. (7)
Для плоского конденсатора, (см. рис. 2), 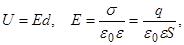
тогда по формуле (7) можно найти 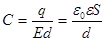 , (8)
, (8)
где 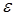 – диэлектрическая проницаемость вещества между пластинами.
– диэлектрическая проницаемость вещества между пластинами.
На электрических схемах электрические конденсаторы обозначают так: a) рис. 3. а - конденсатор постоянной емкости,
б) рис. 3.б- конденсатор переменной емкости,
в) рис. 3. в - подстроечный конденсатор.

|
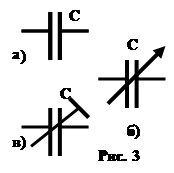














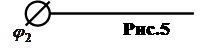 |
 При параллельном соединении конденсаторов, (см. рис. 4) общий заряд qΣ= q1+q2+…+qn.
При параллельном соединении конденсаторов, (см. рис. 4) общий заряд qΣ= q1+q2+…+qn.
Используя формулу (7), находим, что UСΣ= UC1+UC2+…+ UCn, откуда СΣ= C1+C2+…+ Cn=ΣCi (9)
При последовательном соединении конденсаторов, (см. рис. 5) UΣ= U1+U2+…+ Un, что согласно (7) можно переписать так 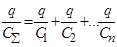 , откуда
, откуда 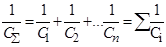 , (10)
, (10)
т.е. суммарная емкость уменьшается.
Дата добавления: 2016-03-04; просмотров: 892;

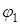 С1 С2 Сn
С1 С2 Сn