Графическое представление цветов в системе RGB

Как мы уже знаем, любой цвет однозначно характеризуется тремя цветовыми координатами–количествами основных цветов системы RGB: Ц®{R,G,B}. Другими словами, цвет является вектором в некотором трехмерном пространстве. Естественно считать, что все цветовые векторы имеют общее начало, которое соответствует «нулевому количеству цвета» – чёрному цвету.

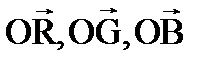
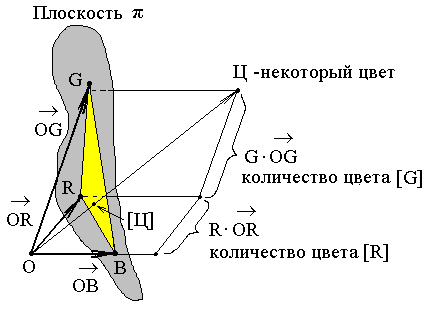
Рисунок 52 – графическое представление цвета в системе RGB

Направим векторы основных цветов произвольным образом, но так, чтобы они не лежали в одной плоскости: Цветовые векторы складываются по обычным правилам, следовательно:

§ Если цвет Ц описывается положительными количествами основных цветов, то его цветовой вектор будет лежать внутри треугольной пирамиды, построенных на векторах 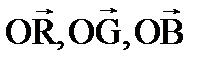. Если одна из координат вектора будет отрицательна, то вектор расположится вне пирамиды.

§ Так как при аддитивном сложении цветов никогда не образуется чёрный цвет, то не существует цветовых векторов с диаметрально противоположными направлениями. Поэтому всевозможные цветовые вектора заполняют не всё пространство, а лишь некоторую его часть.

§ Рассмотрим треугольник ΔRGB, полученный при соединении концов векторов основных цветов - так называемы «треугольник единичных цветов». Концы векторов, соответствующих всевозможным единичными цветами [Ц] (цветам, для которых модуль цвета m равен единице) будут лежать в плоскости π,содержащей данный треугольник. Действительно, уравнение для координат точки, принадлежащей плоскости π и уравнение для координат вектора единичного цвета совпадают: r+q+b =1

Координаты {R,G,B} векторов Ц, соответствующих различным спектрально-чистым цветам были экспериментально определены Райтом и Гилдом. По известным координатам можно построить эти вектора, и тем самым нанести на плоскость π точки всех существующим в природе чистых цветов – получить так называемый «цветовой график»:

Цветность произвольной смеси монохроматических излучений всегда изображается точкой {r, g, b}, лежащей внутри фигуры, ограниченной замкнутой линией BFGRB. Поэтому данная фигура называется «поле реальных цветов».

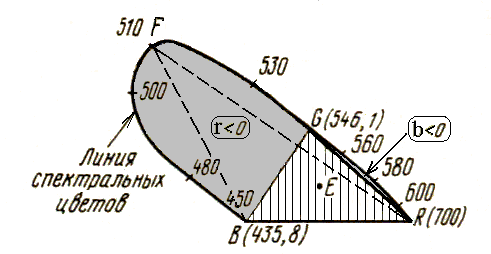
Рисунок 53 - Цветовой график системы RGB

Точкой Е на рисунке обозначен равноинтенсивный белый цвет. Введем еще несколько определений:

Линия, на которой расположены точки цветности всех монохроматических излучений называется линия спектральных цветов или спектральный локус.

Линия, соединяющая точки цветности основного красного и основного синего цветов (т. R и т. B) называется линия пурпурных цветов,на ней расположены максимально насыщенные пурпурные цвета.

Отметим две важные особенности цветового графика:

1. Цветов с отрицательным значением координаты b (закрашенная область « b < 0 » на рисунке 9.4) очень мало, поэтому в большинстве практических расчетов можно считать, что для этих цветов b=0.

2. Цветов с отрицательным значением координаты r(закрашенная область « r < 0 » на рисунке 9.4) очень много: они располагаются вне ΔRGB, на площади ограниченной отрезком BG и кривой BFG.

Указанный недостаток снижает точность вычислений и не может быть устранен выбором вместо RGB другой триады основных цветов, так как не один треугольник с вершинами в точках, соответствующих реальным цветам, не охватывает спектральный локус (смотри, например, ΔRFB).

Система описание цветов XYZ (1931г)

Для упрощения цветовых расчётов, а значит повышения их точности, было крайне желательно избавиться от отрицательных значений координат. Система RGB и все ее аналоги, основанные на триадах спектральных цветов, не смогли обеспечить выполнения такого требования. Поэтому МКО была разработана цветовая система XYZ, в которой реальные цвета были заменены тремя не воспроизводимыми (чисто формальными) цветами, условно названными «Х», «Y» и «Z».

Цвета X,Y и Z лежат вне поля реальных цветов. Они выбраны так, чтобы ΔXYZ полностью охватывал спектральный локус, а расчёты яркости для реальных цветов были наиболее простыми:

1.6

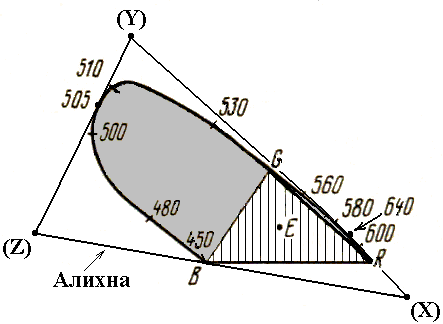
Рисунок 54 Цветовой график системы RGB, с нанесенными основными цветами системы XYZ

Координаты основных цветов системы XYZ (записанные в системе RGB):

(Х) ® {r = 1.2750. g = – 0.2778, b = 0.0028}
(Y) ® {r = – 1.7393, g = 2.7673, b = – 0.0280}
(Z) ® {r = – 0.7431, g = 0.1409, b = 022}

Алихна («бесcветная») – геометрическое место точек нулевой яркости.

Из рисунка 54 следует, что основные цвета «Х» и «Z» лежат на алихне, поэтому они не дают вклада в яркость цвета – для вычисления яркости достаточно знать только количество цвета Y.

Единичные количества для основных цветов данной системы выбрали таким образом, чтобы в сумме основные цвета давали белый цвет Е, причём точно такой же, как и при сложении цветов [R] , [G] и [В]. Данный подход называется «согласование с белым цветом Е»:

[Х] + [Y] + [Z] = [R] + [G] + [B] = Е (9.12)

Итак, в качестве основных цветов системы XYZ, были выбраны следующие цвета:

[Х] ® {r= 2,36461, g= – 0.51515, b= 0.00526} - «ЦВЕТ X»

[Y] ® {r= – 0.89654, g= 1,42640. b= – 0.01441} - «ЦВЕТ Y»

[Z] ® {r= – 0.46807, g= 0.08875, b= 1,00921} - «ЦВЕТ Z»

§ Цветовое уравнение в системе XYZ

В системе XYZ цветовое уравнение имеет тот же вид, что и в системе RGB:

Ц=X×[X] + Y×[Y]+ Z×[Z], (9.13)

где X, Y и Z – количества основных цветов [X], [Y] и [Z] соответственно

Еще раз напомним, что согласно принципу построения рассматриваемой цветовой системы, количества цветов, входящие в уравнение (9.13), есть строго положительные величины.

§ Модуль цвета (m) и координаты цветности {x,y,z} рассчитываются стандартным способом:

m = X+Y+Z, (9.14)

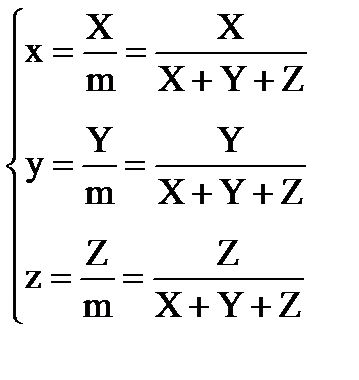(9.15)

Единственное отличие системы ХYZ от системы RGB состоит в том, что координаты цветности в системе XYZ нельзя измерить непосредственно в эксперименте, их выражают через ранее найденные координаты {r, g, b} по формулам:

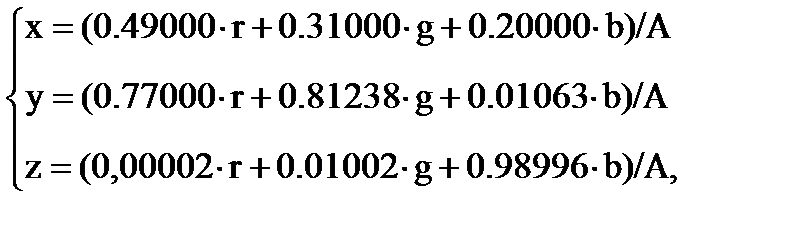, (9.16) где

A = (0.66700×r + 1.13239×g + 1.20058×b) (9.17)

Отметим, что если формулах (9.16) опустить коэффициент «А» (положить Аº1), то все записанные выражения останутся справедливыми, только они будут относится уже не к переводу координат цветности {r,g,b}®{x,y,z}, а к пересчету цветовых координат из одной системы в другую {R,G,B}®{X,Y,Z}.

§ Получим выражение для световогопотока в системе XYZ:

(1) Используем факт согласования систем RGB и XYZ с единичным белым цветом Е :

Система RGB ® Ф_Е = 1·Ф_R + 1·Ф_G + 1·Ф_В (А)

Система XYZ [2] ® Ф_Е = 1·Ф_X + 1·Ф_Y + 1·Ф_Z = Ф_Y (Б)

Приравняв выражения (А) и (Б), находим Ф_Y :

Ф_Y = Ф_R+Ф_G+Ф_В »1.00 лм + 4.59 лм + 0.06 лм=5.65 лм

Точное значение: Ф_Y =5.6508 лм

(2) Зная Ф_Y, выражаем световой поток в системе XYZ:

Ф_[Ц] = Y·Ф_y =5.6508·Y (9.18)

Записанная формула позволяет по известным координатам {X, Y, Z} определить световой поток для заданного цвета. Для единичных цветов в формулу (9.18) вместо «Y» необходимо подставлять «у». Так как точное знание количества некоторого цвета (то есть точное знание светового потока) не влияет на его качественные характеристики, иногда множитель «5.6508» опускают. В этом случае полагают

Ф_[Ц]= Y (9.19)

Величина «Ф_[Ц]» носит уже относительный характер. Естественно, так же относительный характер будет носить и вычисленная по этому световому потоку яркость В. Чтобы отличить яркость, вычисленную по упрощенной формуле (9.19), от полученной по точной формуле (9.18), «яркость по упрощенной формуле» еще называют « относительная яркость».

§ Удельные координаты для монохроматических излучений (кривые сложения) в системеXYZ

Величины 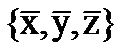в системе XYZ получают расчётным путём. Последовательность действий – совершенно аналогична вычислениям в системе RGB[3]. Имеем:

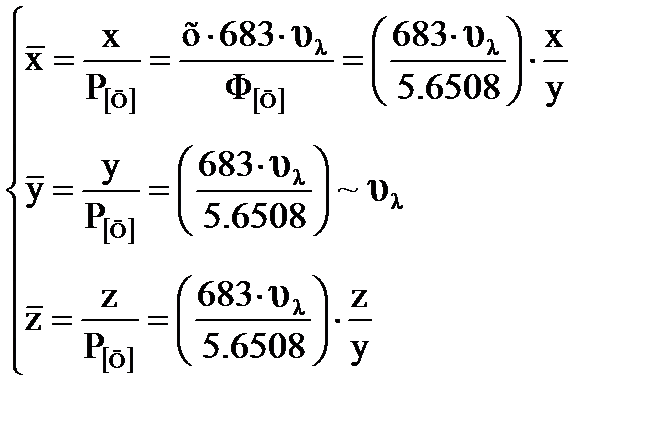(9.20)

Обратите внимание на важную особенностью формул (9.20) – удельная координата 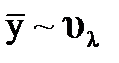. Этот факт упрощает расчёты и позволяет произвести независимую проверку.Результаты вычислений изображены на рисунке 9.7. Видно, что удельные координаты 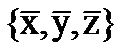для всех излучений в системе XYZ всегда положительные!

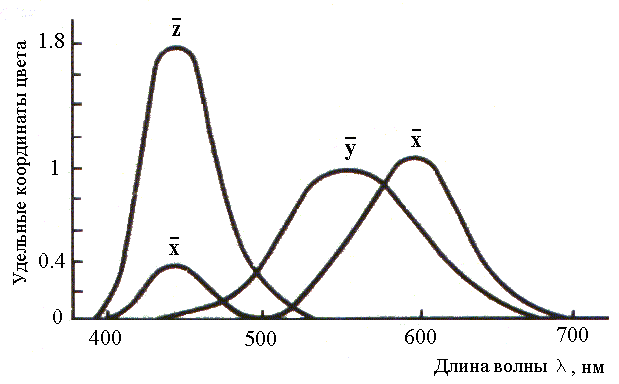
Рисунок 51 –удельные координаты цвета для всех спектрально-чистых цветов в системе CMYK. Мощность: 1/683 Вт

Данный график показывает, в каких количествах необходимо смешать основные цвета системы XYZ (с учетом единичных количеств), чтобы воспроизвести цвет монохроматического излучения с длиной волны λ и мощностью 5.6508 / 683 Вт

Рисунок 51 иллюстрируетудельные координаты спектральных цветов с различной длиной волны (в системе XYZ)

Точно так же, как и в системе RGB, общий множитель в формулах (9.20) – в данном случае это «683 / 5.6508» – при вычислениях часто опускают: он не важен для расчета качественных характеристик цвета. Чтобы понять, опущен ли множитель или нет для конкретных кривых сложения, достаточно посмотреть на кривую 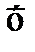: если максимальное значение 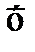равно единице, значит множитель опущен. Пользуясь данным простым критерием, мы легко заключаем, чтопри построении графика 52 общий множитель действительно был опущен.