Цветовой атлас Рабкина

Таблица из атласа Рабкина, позволяющая практически измерить цвет. Половина каждого кружочка в таблице вырезана, другая закрашена соответствующим тоном. Подкладывая под таблицу исследуемый образец, находят совпадение цветового тона на таблице и тона, видимого сквозь прорезь. Затем в ключе-справочнике находят основные характеристики этого цвета

Рисунок 49 – цветовой атлас Рабкина

В основу своей системы Е. Рабкин положил пространственную модель в виде двойного конуса, в вершинах которого располагаются черный и белый цвета, а по окружности общего основания — оптимально насыщенные цвета ахроматического ряда, насыщенность которых убывает по направлению к центру. Сечение конуса вдоль оси дает ряд треугольников одного цветового тона, но различных по светлоте и насыщенности. В атласе Рабкина представлено 12 таких сечений в виде треугольников, состоящих из 45 полей одного цветового тона и 10 ахроматических полей, от белого до черного.

Описанная методика весьма далека от совершенства, она позволяет лишь приблизительно фиксировать цвета, но при этом все же значительно точнее, нежели при простом визуальном наблюдении. Измерения цвета, которые производятся при помощи сравнения испытуемого пятна с неким фиксированным эталоном, конечно, будут также иметь ограничения, зависимые и от субъективных условий наблюдений, и от объективных моментов, связанных с различием условий освещения, фактуры и т. п. При измерениях нужно учитывать также, что в красочном слое картины происходят изменения.

С точки зрения возможности измерения все сложное многообразие способов использования цвета в живописи можно условно разделить на три группы:

1. Цвет используется в его «чистом» виде, никак, ни в каком направлении не модифицированным. В этом случае каждый тон определяется через обозначения его светлоты, цветового тона и насыщенности сравнительно легко, с помощью принятых обозначений; его можно по этим обозначениям достаточно точно воспроизвести при отсутствии оригинала.

2. Цвет модифицируется путем высветления и затемнения. Здесь с успехом может быть использована для измерения и описания система Оствальда.

3. Третий тип использования цвета в художественном произведении подразумевает «перетекание», градирование цвета по всем его характеристикам одновременно. Он представляет наибольшие трудности для фиксации. В этом последнем случае измерения представляют наибольшую сложность и будут менее точными, но отнюдь не бесполезными.

Пока речь идет об изучении цвета в его элементарной основе, абстрагировано от его эстетической оценки, без учета эмоциональных моментов, сопровождающих его восприятие, не только возможно, но и нужно такое строгое его определение. Все же эмоционально-субъективные наслоения, сопровождающие процесс восприятия, — это уже следующий уровень, следующая задача, которая тем серьезнее и научнее будет решаться, чем объективнее и точнее будут данные, полученные на первом уровне.

4.2 Теоретические основы измерения цветов

Система описания цветов RGB (1931г)

Согласно первому закону аддитивного смешения цветов, любой цвет Ц может быть выражен через три линейно-независимых цвета:

Ц=R×[R] + G×[G]+ B×[B], (9.1)

где R, G и В – количества основных цветов [R], [G] и [B] соответственно. Напомним, что количества цветов являются алгебраическими величинами, то есть входят в выражение со знаком «+» или «-». Данная запись цвета называется «цветовое уравнение», а входящие в неё количества цветов называется «координаты цвета в трихроматичной (трёхцветной) системе». Резолюцией МКО в качестве основных цветов системы RGB выбраны следующие излучения в определенных количествах:

[R] → λ_R=700.0 нм; Ф_R= 1.00 лм - «КРАСНЫЙ»

[G] → λ_G=547.1 нм; Ф_G=4.59 лм - «ЗЕЛЕНЫЙ»

[В] → λ_В=435.8 нм; Ф_В=0.06 лм - «СИНИЙ»

Величины световых потоков Ф_i были специально подобраны таким образом, чтобы три основных цвета, взятые в равных количествах, давали в сумме единичный белый цвет «Е»:

[R]+[G]+[B]=E (9.2)

Такой белый цвет в литературе называют «равностимульный (или равноинтенсивный) белый цвет», чтобы подчеркнуть тот факт, что он сформирован взятыми в равных количествах основными цветами.

Ясно, что при удвоении количества цветов суммарный цвет белый цвет так же «удвоится»:

2×[R]+2×[G]+2×[B]=2×Е – белый цвет в «удвоенном количестве»

Введем несколько определений:

1). Модуль цвета (m)

По определению, модуль цвета m равен сумме трех координат данного цвета:

m = R+G+B (9.3)

Пример с белым цветом показывает, что цветовой модуль m характеризует цвет с количественной стороны

2). Координаты цветности {r, g, b}

По определению, координаты цветности {r, g, b} - это отношение координат цвета к его модулю:

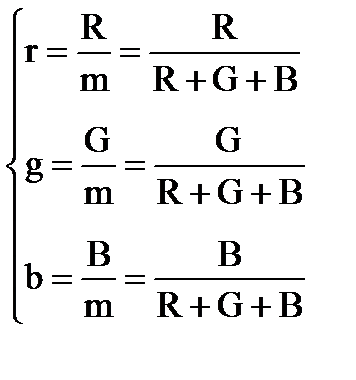(9.3)

Введенные таким образом координаты цветности {r, g, b} определяют цвет с качественной стороны, то есть описывают оттенок цвета (тон + насыщенность). Можно сказать, что координаты цветности представляют собой координаты некоторого цвета, взятого «в единичном количестве» - так называемого «единичного цвета».

Из определения координат цветности ясно, что r+g+b=1. Следовательно, для описания цветового оттенка достаточно задать только две координаты цветности, например {r,g}, недостающую координату легко выразить: b=1- (r + g). Используя данное свойство координат цветности, все тона можно изобразить в виде точек на плоскости.

Воспользовавшись формулами (9.3) перепишем цветовое уравнение в другом виде:

Ц = R×[R]+G×[G]+B×[B] = m×r×[R]+m×g×[G]+m×b×[B] =

= m×( r×[R]+g×[G]+b×[B] )=m×[Ц], (9.4)

где [Ц]= r×[R]+g×[B]+b×[B] – (по смыслу) некоторый единичный цвет,

(9.5)

m= R+G+B – модуль цвета

Видно, что модуль цвета показывает, в каком количестве необходимо взять единичный цвет [Ц] (соответствующий тону и насыщенности цвета Ц), чтобы получить интересующий нас цвет. Отметим, что выражение (9.5), описывающее единичный цвет, по своей форме совершенно аналогично цветовому уравнению (9.1). Поэтому (9.5) принято называть «цветовое уравнение для единичного цвета [Ц]».

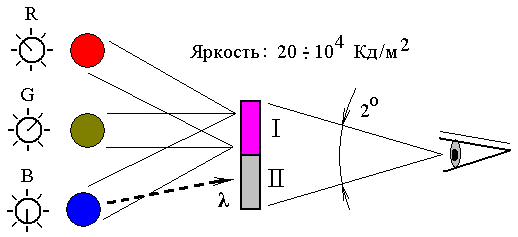
Рисунок 50– схема эксперимента Райта и Гилда.

Для выполнения практических расчётов, В. Райт и Ж. Гилд в эксперименте определили координаты цветности для всех монохроматических излучений (всех чистых цветов). На рисунке 9.1 приведена схема их эксперимента.

В области экрана I смешиваются излучения основных цветов.

В области экрана II наблюдатель видит излучение с длиной волны λ, координаты цветности которого требуется определить.

Указанная на рисунке яркость экрана необходима для обеспечения нормальной работы колбочек глаза.

Управляя регуляторами количества для всех трех основных цветов, экспериментатор должен выровнять цвет полей I и II - добиться цветового тождества излучений в обеих областях поля зрения.

Отметим некоторые особенности измерений:

§ Регуляторы количества основных цветов были градуированы в соответствии со значениями единичных цветовых потоков Ф_R , Ф_G и Ф_В.

§ Как мы уже знаем, цвет спектрально-чистого излучения не всегда может быть воспроизведен путём аддитивного смешивания трех основных излучений. Поэтому в некоторых случаях к исследуемому излучению можно было подмешивать одно из основных излучений, с целью «разбавления» (для снижения насыщенности исследуемого цвета). Пусть, например, для целей разбавления использовалось излучение синего цвета ( показано пунктирной стрелкой на рисунке) в количестве B₁. В этом случае, после установлении цветового тождества получаем:

§

Ц(λ) + B₁×[B] = R×[R] + G×[G] + B₂×[B] Þ

Ц(λ)=R×[R]+G×[G]+ (B₁-B₂)×[B] , (9.6)

где R, G, и В =B₁-B₂ - количества основных цветов, измеренные в «единичных цветовых потоках» (то есть положения ручек регуляторов основных цветов).

Зная количества основных цветов, необходимые для установления цветового тождества, экспериментаторы легко рассчитали координаты цветности:

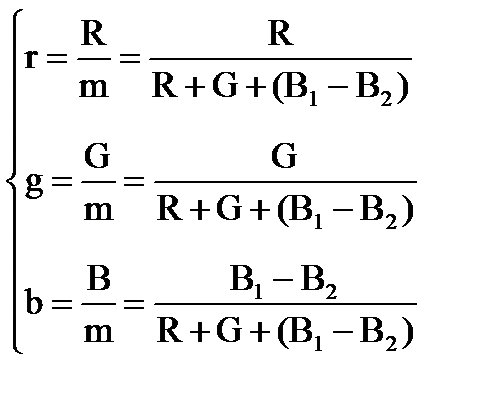(9.7)

3). Удельные координаты .

При выполнении расчетов, часто оказываются полезны так называемые «удельные координаты» . В литературе их могут называть по-разному: «удельные координаты спектральных излучений постоянной мощности», (применительно к графикам) «кривые сложения».

Удельные координаты - это координаты цвета, световой поток которого имеет мощность 1 Вт.

Таким образом, имеется три типа координат цвета:

Координаты цвета:{R,G,B}–полная характеристика цвета Ц

Удельные координаты цвета: – характеризуют цвет того же оттенка, что и Ц, но с мощностью 1Вт

Координаты цветности: {r, g, b} – характеристика единичного цвета [Ц], соответствующего данному Ц

Чтобы рассчитать удельные координаты некоторого спектрально-чистого излучения Ц с длиной волны l, поступают следующим образов:

§ находят координаты {r, g, b}, для соответствующего этому излучению единичного цвета [Ц]

§ вычисляют мощностьединичного цветаP[Ц](выраженную в Ваттах!):

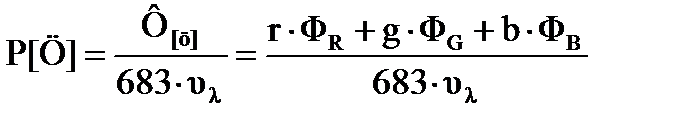, (9.8)

где Ф_[ц] – световой поток, соответствующий единичному цвету [Ц], Ф_i – единичные световые потоки для трех основных цветов.

§ каждую из координат {r, g, b} единичного цвета [Ц] делят на эту мощность:

(9.9)

Итак, выражения (9.9) позволяют нам по известным координатам цветности {r, g, b} некоторого спектрально-чистого излучения вычислить его удельные координаты - то есть координаты цветас тем же оттенком, но обладающего мощностью 1Вт. Обратите внимание на тот факт, что множитель «683» является общим для всех трех удельных координат: он входит в формулы для каждой из них. Легко понять, что общий множитель не важен для расчёта качественных характеристик цвета, поэтому его часто опускают.

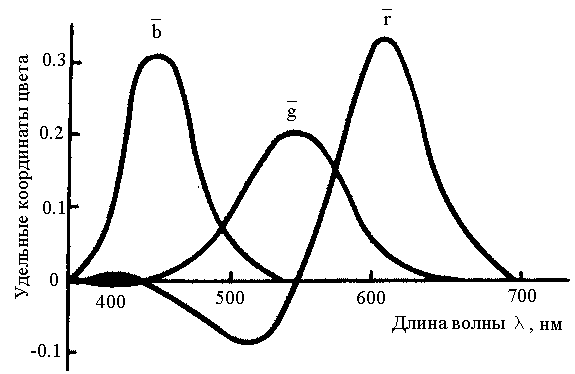
Рисунок 51 –удельные координаты цвета для всех спектрально-чистых цветов в системе RGB. Мощность: 1/683 Вт

Данный график показывает, в каких количествах необходимо смешать основные цвета системы RGB (с учётом единичных количеств Ф _i ), чтобы воспроизвести цвет монохроматического излучения с длинной волны l и мощностью 1/ 683 Вт.

Удельные координаты спектральных цветов с различной длиной волны (в системе RGB)

Пользуясь кривыми сложения легко расчитать координаты спектрально-чистого цвета (монохроматического излучения) с длиной волны l и мощностью Р:

(9.10)

Если излучение не монохроматическое, а обладает сложным спектром, вычисления усложняются. Такое излучение представляет собой совокупность большого числа световых волн с различной длиной l и обладающих мощностью dP_l (dP_l = Р_l×dl - «мощность излучения, обладающего длиной волны вблизи λ»[1]). Координаты цвета в этом случае – есть алгебраическая сумма координат цвета для каждой из волн, вычисленных по формуле (9.10). Таким образом, для излучения со сложным спектром получаем следующую формулу:

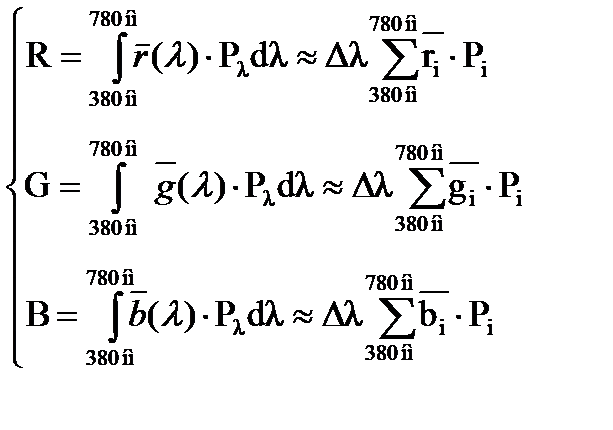(9.11)