Нелинейная двухэлементная модель цветовосприятия

В основе заложены два принципа:

· Имеются только два типа светочувствительных элементов сетчатки глаза — однотипные колбочки и палочки;

· Осуществляется нелинейность процессов формирования сигналов цветности (без суммирования или вычитания).

Первое: цвет должен выражаться конкретным, объективным физическим параметром. Законы физики едины как для неживой, так и для живой материи. Мозг в переработке сигнала цветности участия не принимает.

Второе: так, как воспринимаются и цвета отсутствующие в спектре, длина волны не может служить параметром для определения цвета, а её размерность в формуле, определяющей сигнал цветности, сокращается. Исходя из этого, следует, что в данной формуле размерность длины волны должна находиться и в числителе, и в знаменателе. Таким образом, сигнал цветности представляет функцию от отношения сигналов двух, четырёх или любого чётного числа фоторецепторов. Вычисление сигнала цветности должно производиться нелинейными функциональными зависимостями.

Суть теории заключается с следующем:

Колбочка выступает как светоприемник, разделенный на две части, одна чувствительна к красному цвету, другая – к зеленому. Если такой приёмник расположен за призмой или линзой (хрусталик), то, оказывается, что нет необходимости даже специально настраивать его на соответствующие длины волн. Достаточно его размеры, место контакта и расположение выбрать соответствующим образом. Это хорошо видно на рис. 25 а. В результате преломления «красные» лучи будут падать на красночувствительную область, «зелёные» - на зелёночувствительную, «жёлтые» - в одинаковой степени на обе.

Если светоприёмник расположить вдоль оси направления света, то раскладывать излучение в спектр нет необходимости. Для этого достаточно использовать низкокачественную линзу с большой хроматической аберрацией, например хрусталик. Его «недостаток» окажется не только полезным, но и необходимым. Это хорошо видно на рис. 25 b.

Ближе всего к - хрусталику - располагается зелёночувствительная область, центр которой расположен в фокусе зеленых лучей. Красночувствительная область находится дальше. При этом используется ещё одно физическое свойство веществ: более коротковолновые лучи поглощаются быстрее; длинноволновые же, для того чтобы их поглотилось столько же, должны пробежать путь длиннее. Такой приёмник может считаться оптимальным и может давать достаточное количество информации как о количественном, так и о спектральном составе света.

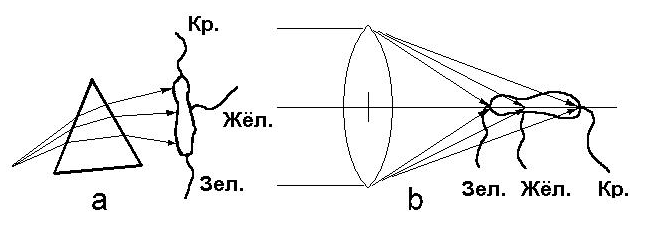
Рисунок 25-Схема восприятия цветов в нелинейной теории цвета

Нужна ли другая колбочка с парой «желтый-синий»? Желтый сигнал уже есть. Может ли палочка играть роль синечувствительного элемента. Может, в ней есть чувствительный к синезеленому спектру пигмент. Смесителем выступают нейроны, которые связывают палочки и колбочки.

Рисунок 26- Эквивалентная схема нелинейной модели: 1 - колбочка, 2 - палочка, 3 - узел сравнения

Противоположная пара жёлтый - синий в смеси дает белый свет, а пары зелёный - красный нет. Синий, зелёный и жёлтый - спектральные тона. Однако чистый красный противоположным быть не может. И вот почему.

И рецепторы, и нейроны, и нервные волокна состоят из белков. И те, и другие поглощают интенсивно ультрафиолетовые лучи и немного сине-фиолетовые. Не удивительно, что была обнаружена реакция нейронов на свет. Часть попавшего в глаз синего света поглотится нейронами. «Синий» сигнал не изменится, «зелёный» пренебрежительно мал, а вот «красный» изменится заметно. К «красному» сигналу окажется подмешанным и «синий» сигнал нейрона.

Таким образом, при воздействии на колбочку белого света противоположным зелёному окажется не красный, а красно-синий, пурпурный.

3.4 Цветокоординатная система

Цветокоординатная система нелинейной модели и кривая видности глаза. Кривая, описывает положение спектральных цветов (непрерывного спектра полученного разложением призмой белого солнечного света) на координатной плоскости.

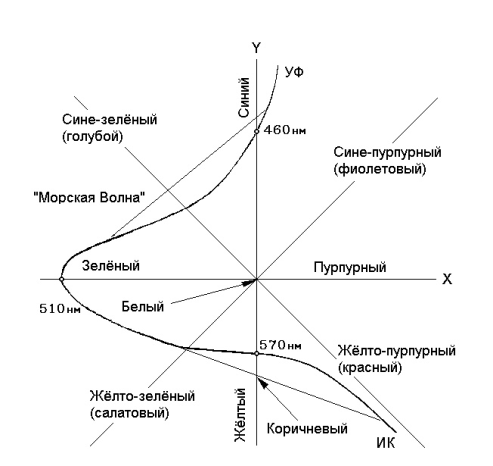
Рисунок 27-Цветокоординатная система

Исходя из этой теории, белый цвет можно получить смешиванием всего двух цветов. Таких пар цветов может быть неограниченное количество. Причём, эти цвета могут быть спектральными, а могут и не быть таковыми. Логично принять точкой начала координат системы, точку соответствующую белому цвету. В этой точке цветовые сигналы равны нулю. Реально это будет точка серого цвета, зависит от яркости, которая может изменятся от чёрного до белого (яркость это третья координата перпендикулярная нашей плоскости). Если нанести на линейный спектр пары цветов, при смешивании дающие белый цвет, то они должны быть диаметрально противоположны (относительно белого) на нашей цветокоординатной системе. Нанесём точки всех пар цветов (образующих при смешении белый цвет) на нашу плоскость (при постоянной яркости). Получим некую кривую, описывающую положение спектральных цветов (непрерывного спектра полученного разложением призмой белого солнечного света) на координатной плоскости. Теперь проведём линии из центральной точки (белый цвет) в точки на кривой спектра с наиболее привычными нам цветами. Обнаружим закономерность: например линия жёлтый — синий проходит через центр нашей системы координат (белый). См. Рис. 27.

Кроме того заметим, что линия зелёный-белый, перпендикулярна линии жёлтый — синий. Если продлить линию зелёный-белый дальше, то она попадает на «пурпурный» цвет, который отлично воспринимает наш глаз, но которого нет в спектре. Примечательно, что пурпурный цвет на нашей системе расположен между красным и синим цветами, смешивая которые мы можем получить все оттенки пурпурного. Несложно заметить и проверить, что любой цвет на полученной плоскости можно получить смешиванием граничащих с ним цветов. Любой цвет воспринимаемый (и даже не воспринимаемый) нашим глазом, можно легко выразить в этой системе вектором, идущим из точки начала координат (белого), в точку полученную геометрической суммой цветовых сигналов с координатой - Х (соотношение зелёно-пурпурного), координатой - У (соотношение синего-жёлтого) и сигнала яркости с координатой - Z.

Нелинейная модель позволяет выразить насыщенность в виде физического параметра, величину которого можно измерить прибором. Для этого сформулировано определение: «насыщенность - это величина, представляющая отношение (вектора) геометрической суммы цветовых сигналов к сигналу (вектору) яркости». Ни одна другая теория зрения, не может дать физическую или математическую интерпретацию данного параметра.

Огромное разнообразие световых излучений в природе от светящихся тел и несветящихся предметов, вызывающих у человека цветовые ощущения, может привести к мысли, что во всех этих излучениях и ощущениях нет никакой системы и порядка. Но это не так. Со времени Ньютона ученые пытаются найти закономерности, определить причины и следствия, построить модели. Первую систематизацию цветов еще в 1680 г. провел Ньютон. Он расположил цвета в том порядке, в котором они находятся в спектре или радуге, но расположил их по кругу. Так возникла первая цветовая модель — цветовой круг Ньютона.

Цветовой круг - способ представления непрерывности цветовых переходов, а также модели HSB (англ. Hue, Saturation, Brightness - оттенок, насыщенность, яркость). Сектора круга окрашены в различные цветовые тона, размещенные в порядке расположения спектральных цветов, причем пурпурный цвет связывает крайние (красный и фиолетовый) цвета.

Это своеобразное мнемоническое правило, которое помогает ориентироваться в пространстве цветов, создавать нужный оттенок в любой цветовой модели.

3.5 Цветовая система Ньютона-цветовой круг

Цветовой круг, составленный из семи секторов: красного, оранжевого, желтого, зеленого, голубого, синего и фиолетового.

Рисунок 28-Историческое изображение цветового круга Ньютона

Приемы смешения, которыми пользовался Ньютон, также не были безупречными. Но все законы оптического смешения были фактически предсказаны им. Он заметил и тот факт, что смешение фиолетового и красного цвета дает пурпурные цвета, которых нет в спектре. Таким образом, множество цветов оказалось не только непрерывным, но и замкнутым. Увидел Ньютон и то, что смешение не близких по спектру цветов всегда ведет к потере насыщенности, к подмеси белого (серого). Идея цветового круга была столько же естественным, сколько и удивительным следствием экспериментов гениального физика по смешению цветов, так же как идея самого смешения - естественным и удивительным следствием наблюдений над разложением солнечного луча.

По окружности цветового круга расположены непрерывно изменяющиеся но цветовому тону насыщенные цвета - спектральные и пурпурные. Против пурпурно-красного расположен зеленый цвет, против красного - сине-зеленый, против оранжевого - синий и против желтого - фиолетовый. На каждом радиусе расположены цвета одного цветового тона, непрерывно изменяющиеся по насыщенности от спектрального или пурпурного до белого, расположенного в центре круга. Изменение цвета по светлоте в цветовом круге не учитывается.

На цветовом круге легко наглядно показать три закона оптического смешения цветов. Согласно идее Ньютона, цвет смеси находится (по принципу центра тяжести) на прямой, соединяющей смешиваемые цвета, ближе к тому цвету, которого в смеси "больше".

3.6 Цветовой круг Гете

Позднее (конец XVIII в.) Гете построил свой цветовой круг. Его исследования расходились с позицией Ньютона. Последовательность цветов в цветовом круге Гете – не замкнутый спектр, как у Ньютона, а три пары цветов: три основных цвета (красный, желтый, синий), чередующихся с тремя дополнительными (оранжевый, зеленый, фиолетовый). Последние получаются путем попарного смешения рядом лежащих основных цветов. Гете считают родоначальником физиологической оптики и науки о психологическом воздействии цвета.

Ответ опять же каждый может найти сам в простейшем опыте. Возьмите три кружка (квадратика, треугольника – чего захотите), окрашенных чистыми CMY. Расположите один из них на белом фоне. Эффект будет точнее, если вы осветите кружок ярким направленным белым светом. Но можно обойтись обычным освещением. Все будет видно, но несколько бледнее. Смотрите пристально на кружок примерно 10 секунд. Потом уберите его с фона и, расслабив глаза, продолжайте смотреть на белый фон. Проделайте то же самое с другими кружками. Вы увидите, что на месте голубого кружка появляется красный послеобраз, на месте пурпурного – зеленый, на месте желтого – фиолетовый.

Гете рассматривал цвет как результат взаимодействия света и тьмы. Он не стал создавать сложные условия для воспроизведения эксперимента Ньютона. Он просто нарисовал белую точку на черном фоне и в призме возник… ньютоновский семицветный спектр. Гете не удовлетворился этим явлением и такую же точку, но уже черную, нанес на белую бумагу. И снова взглянул в призму. Результат оказался еще неожиданнее – спектр появился вновь, но цвета в нем были другие…

Рисунок 29-Визуальное представление экспериментов Гете

Гете описывает желтый, как «ближайший к свету. Он возникает благодаря самому незначительному ослаблению последнего…».

Итак, желтый – минимальное затемнение света (цвет Солнца).
Голубой – максимальное высветление тьмы (цвет Неба). Гёте иногда называет спектральный голубой «зеленовато-голубым», чтобы подчеркнуть его абсолютную холодность и отсутствие малейшего внедрения в него красного.

Желтый и голубой приняты Гете за основные, исходные. Он называет их цветами со стороны света.

Третий гетевский основной цвет – пурпур. Что происходит в этих точках с цветными полосами, возникающими на границе белого и черного? В узком пространстве белой точки желтый и голубой, накладываясь, смешиваются в зеленый. В центре черной точки соединяются красный и фиолетовый. И здесь, наконец, мы можем наблюдать пурпурный. В отличие от зеленого, пурпур не рождается путем смешения соседних цветов.

Каждый, вооружившись призмой, может пронаблюдать то же самое и собственными глазами увидеть все эти цветовые чудеса.

Рисунок 30-Основные цвета Гёте

Из картины, представшей в белой и черной точке, Гете сделал логичный вывод, что условия возникновения цветов в призме рассмотрены теперь полностью, а спектральный круг можно, наконец, замкнуть.

Рисунок 31-Замкнутый круг Гёте

А это один из кругов, нарисованных самим Гёте:

Рисунок 32- Круг, нарисованный Гете

3.7 Цветовой круг Оствальда

В конце XIX в. В. Оствальд создал свой цветовой круг, который содержит двадцать четыре цвета. В цветовом круге представлены только хроматические цвета, здесь нет белых, серых и черных цветов.

Цвета, расположенные на круге напротив друг друга (на концах одного диаметра), называют дополнительными (комплиментарными). При смешении в определенной пропорции пара дополнительных цветов дает ахроматический цвет (черный для красок или белый для световых лучей).

Любые 3–4 цвета, расположенные на круге последовательно, называют близкими (смежными).

Если представить в цветовом круге равнобедренный треугольник, то цвета, которые окажутся на его вершинах, образуют триады. Триады – три цвета, равноотстоящие друг от друга на цветовом круге.

Большой цветовой круг Оствальда применяется для образования гармоничных сочетаний из двух, трех, четырех цветовых тонов. Принцип пользования кругом аналогичен принципу пользования шестисекторным с помощью стрелок.
Цветовой круг Оствальда дает более полную возможность составить необходимые сочетания. Например: если в композиции имеется предмет с насыщенным цветом, то к нему можно подобрать другой предмет, цвет которого усилил бы ощущение насыщенности цвета первого.

Необходимо помнить, что с помощью фона можно усилить звучание композиции в целом, отдельных ее частей или предметов. Серый, черный и белый фон часто образует приятное сочетание, но белые предметы на светлом фоне пропадают. Бежевые цвета теряются на сером фоне.

На рис. 33 изображен 12-секторный цветовой круг И. Иттона с включенными в него треугольником, представляющим три основных независимых цвета, и шестигранником, представляющим смеси этих цветов , 12-лучевая цветовая звезда И. Иттона, демонстрирующая ступенчатый переход от чистых хроматических цветов к разбеленным и зачерненным

Рисунок 33- Большой цветовой круг Иттона

Вот как он сам поясняет принципы, на которых он создал свой круг: "Для введения в систему цветового конструирования создадим двенадцатичастный цветовой круг, опираясь на основные цвета - жёлтый, красный и синий. Как известно, человек с нормальным зрением может определить красный цвет, не имеющий ни синеватого, ни желтоватого оттенка; жёлтый - не имеющий ни синеватого, ни красноватого тона, и синий, не имеющий ни зеленоватого, ни красноватого оттенка. При этом, изучая каждый цвет, следует рассматривать его на нейтральном сером фоне.
Основные цвета должны быть определены с максимально возможной точностью. Три основных цвета первого порядка размещаются в равностороннем треугольнике так, чтобы жёлтый был у вершины, красный справа внизу и синий - внизу слева. Затем данный треугольник вписывается в круг и на его основе выстраивается равносторонний шестиугольник. В образовавшиеся равнобедренные треугольники мы помещаем три смешанных цвета, каждый из которых состоит из двух основных цветов, и получаем, так разом, цвета второго порядка:

жёлтый + красный = оранжевый
жёлтый + синий = зелёный
красный + синий = фиолетовый.

Все цвета второго порядка должны быть смешаны весьма тщательно. Они не должны склоняться ни к одному из своих компонентов. Запомните, что это нелёгкая задача - получить составные цвета посредством их смешения. Оранжевый цвет не должен быть ни слишком красным, ни слишком жёлтым, а фиолетовый - ни слишком красным и ни слишком синим. Затем на некотором расстоянии от первого круга мы чертим другой и делим полученное между ними кольцо на двенадцать равных частей, размещая основные и составные цвета по месту их расположения и оставляя при этом между каждыми двумя цветами пустой сектор. В эти пустые сектора вводим цвета третьего порядка, каждый из которых создаётся благодаря смешению цветов первого и второго порядка, и получаем:

жёлтый + оранжевый = жёлто-оранжевый
красный + оранжевый = красно-оранжевый
красный + фиолетовый = красно-фиолетовый
синий + фиолетовый = сине-фиолетовый
синий + зелёный = сине-зелёный
жёлтый + зелёный = жёлто-зелёный.
Таким образом, возникает правильный цветовой круг из двенадцати цветов, в котором каждый цвет имеет своё неизменное место, а их последовательность имеет тот же порядок, что в радуге или в естественном спектре.

3.8 Опыты Юнга

Трехкомпонентная теория была развита Томасом Юнгом (1773—1829). Если Ньютон показал, что разные цвета можно получать смешением других цветов, то Юнг ввел понятие о трех основных цветах и простым, изящным опытом показал, как их смеше­нием можно получить другие цвета. Взяв три проек­ционных фонаря, Юнг направил их свет на белый экран так, чтобы проекции кругов частично перекры­вались (рис. 34).

Рисунок 34- Опыт Юнга

В три фонаря были вставлены све­тофильтры: зеленый, красный, синий. В середине картины перекрывались изображения всех трех цве­тов и появлялся белый цвет. Перекрытие синего и зеленого давали голубой, зеленого и красного - желтый, красного и синего – пурпурный.

Юнгу было ясно, что трехкомпонентность цвета нельзя объяснить физическими свойствами самого света. Значит, она зависит от свойств глаза. Глаз имеет три приемника с различными чувствительностями к разным областям спектра. Суммирование степени их возбуждения светом дает ощущение того или иного цвета.

3.9 Колориметр Максвелла

Д. К. Максвелл (1831 —1879), создавший электро­магнитную теорию света, очень интересовался цве­товым зрением. Максвелл построил первый колори­метр, в котором измеряемый цвет Ц освещал половину поля зрения, в то время как другая освещалась смесью трех излучений: красного, зеленого и синего. Интенсивности каждого из излучений можно было изменять до тех пор, пока не устанавливалось равен­ство цвета обоих полей прибора. После установления равенства можно было написать уравнение

Ц = аК + bЗ + сС, (1)

где Ц — измеряемый цвет, а коэффициенты а, b и с - величины, пропорциональные интенсивностям крас­ного (К), зеленого (3) и синего (С) излучения соот­ветственно. У Максвелла эти коэффициенты были равны или пропорциональны ширине щели, пропускающей каждое из трех излучений к полю сравнения.

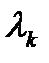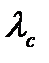За основные Максвелл принял три спектральных цвета с длинами волн = 630 нм, = 528 нм и = 457 нм. Графически смешение цветов Слайд 16

Максвелл изобразил в виде равностороннего треугольника (рис. 35).

Рисунок 35- треугольник Максвелла

Треугольник Д. К. Максвелла — график смешения цветов, отражающий основы трехкомпонентной теории цветового зрения Г. Гельмгольца. Аддитивным смешением монохроматического света определенных длин волн (соответствующих трем первичным цветам — красному, зеленому и синему) можно получить очень широкий диапазон цветов, включающий все цветовые тона разной насыщенности (чистоты)

Стороны треугольника нанесены штрихами, в вершинах лежат излучения с 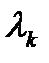, , 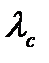. Цвет, получающийся в результате сложения интенсивно-стей, пропорциональных коэффициентам а,b и cдля основных цветов, можно найти по принципу отыска­ния центра тяжести, как и в круге Ньютона. При ра­венстве а = b = с получается белый цвет (центр тре­угольника).

Спектрально-чистые цвета лежат на сплошной линии за пределами штрихового треугольника. При положительных значениях всех трех коэффициентов а, b и c можно получить только цвета, лежащие вну­три треугольника и на его сторонах.

Пусть по правилу сложения сил мы нашли для не­которого цвета Ц его положение на треугольнике Максвелла. Проведя из точки белого цвета W через любую точку Ц прямую до ее пересечения со сплош­ной линией спектрально - чистых тонов, мы получаем длину волны цвета Ц. Чем дальше точка Ц от точки W, тем больше чистота цвета Ц. Таким обра­зом, точка на чертеже дает возможность судить о значениях величин и р для этого цвета. Яркость L зависит от абсолютных значений величин а, b и с.

Давайте сравним:

Рисунок 36- совмещение треугольника Максвелла с 6-ти секторным кругом Гете

Совмещение треугольника Д. К. Максвелла с 6-секторным кругом И. В. Гете. Три первичных цвета (красный, зеленый, синий) в углах треугольника на окружности располагаются под углом 120° друг к другу, в центре дуги, ограничивающей соответствующий сектор цветового круга. Цвета, получаемые смешением монохроматических лучей света первичных цветов — желтый, голубой, пурпурный, проецируются вдоль радиуса окружности из средней точки каждой стороны треугольника на центр дуги соответствующего сектора круга. Последовательность цветов в треугольнике и цветовом круге одинакова

Крупный ученый Г. Гельмгольц (1821 —1894), сде­лавший много открытий в различных областях физи­ки, признал трехкомпонентную теорию зрения, способcтвовал ее развитию, построил свою модель колори­метра. На колориметре Гельмгольца работали Кениг и Дитеричи. Работы по развитию и конкретизации трехкомпонентной теории шли в двух направлениях: поиска трех веществ сетчатки и зависимости чув­ствительности их от длины волны; изучения, чувстви­тельности трех приемников по данным колориметри­ческих измерений.

3.10 Теория светочувствительности Геринга

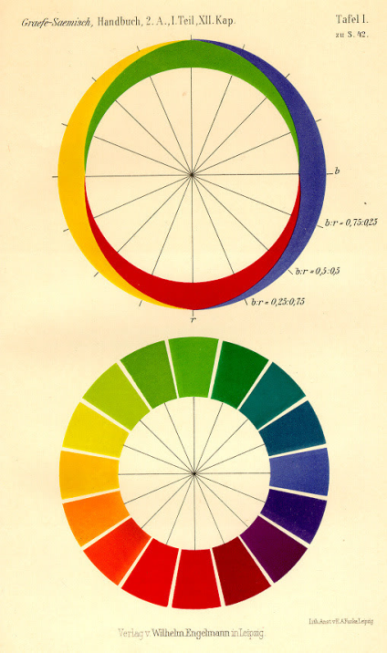
Между 1872 и 1874 годом физиолог Эвальд Геринг (1834-1918) выпустил в Академии Наук Вены "шесть сообщений", озаглавленных "О теории светочувствительности", опубликованных в частном порядке в 1878 году, в которых Геринг оппонирует взглядам Гельмгольца на цветовые явления - в числе основных цветов непременно должен присутствовать желтый, так как наш глаз и его воспринимает как самостоятельный цвет наравне с красным, зеленым и синим. В качестве основных цветов Геринг включает в этот ряд черный и белый. Такой порядок цветов ученый обозначает как «систему натуральных цветовых ощущений». На этой системе сегодня основана N.C.S., Natural Color System (Природная Система Цвета), которая широко используется в мире в качестве инструмента подбора подходящих цветов.

а

б

Рисунок 37- цветовая система Геринга

Основные цвета, расположенные друг напротив друга являются контрастными. При смешивание четырех «основных» чистых цветов получаем дополнительные цвета: лиловый, бирюзовый, оранжевый и салатово-зеленый (см. цветовой круг Геринга). Помимо дополнительных и контрастных, цвета бывают родственными. В цветовом круге имеются четыре группы родственных цветов: желто-красные, желто-зеленые, сине-красные и сине-зеленые.

3.11 Методы образования цвета. Законы Грассмана

Изменить спектральный состав светового излучения, а значит и наблюдаемый глазом цвет, можно только двумя способами: добавив к световому потоку некоторые новые волны или удалив из светового потока некоторых из имеющихся волн. Данные методы синтеза цвета называются соответственно «аддитивный синтез» и «субстрактивный синтез». Итак:

· Аддитивный синтез– метод синтеза, при котором образование цвета происходит в результате оптического сложения двух и более световых потоков. Пример – смешение лучей прожекторов на арене цирка.

· Субстрактивный синтез– метод синтеза, при котором образование цвета происходит вследствие избирательного поглощения части излучений из падающего на тело светового потока. Пример – смешивание красок, краска.

Рисунок 38 – аддитивная и субтрактивная цветовые системы

Аддитивный (слагательный) и субтрактивный (вычитательный) способы оптического смешения цветов: а) получение цветов сложением монохроматических световых потоков цветных источников света — красного, зеленого и синего; в местах попарного перекрывания при проецировании на белый экран образуются желтый, голубой и пурпурный цвета, в центре — белое пятно;

б) получение цветов вычитанием из белого цвета соответствующих излучений при помощи светофильтров пурпурного, голубого и желтого цветов; в местах перекрывания на белом экране образуются красный, фиолетовый и зеленый цвета, в центре черное пятно

Метод, связанный с красками и смешиванием красок (субстрактивный) нам более привычен, мы неоднократно встречались с таким смешиванием в обыденной жизни. Однако, для большей наглядности, рассмотрение начнем с аддитивного метода синтеза.

3.12 Аддитивный синтез цвета

Рисунок 39 – схема аддитивного синтеза цвета

Рассмотрим наглядный пример – сведение на экране лучей трех цветных прожекторов: Зеленого, Красного и Синего. Далее, для краткости всюду будем обозначать цвета первыми буквами названия «З», «К», «С». См. рис 39.

Безусловно, смешивать цвета «со сложением» можно и по-другому. Перечислим все возможные способы:

1). Одновременное смешивание

Одновременное проецирование нескольких цветов в одну область экрана (см. выше).

2). Поочередное смешивание

Попеременное проецирование нескольких цветов на экран или быстрое вращение диска с разноцветными секторами. В этом методе чередование цветов должно быть достаточно быстрым, иначе вместо однородного суммарного цвета будет наблюдаться простое мелькание цветов. Для вращающегося диска ощущение однородной окраски возникает при частоте вращения v ~ 30 сек ^–1 = 1800 мин ^-1.

3). Пространственное смешивание

На экране формирует мозаику, то есть создают множество мелких разноцветных пятнышек или полосок. С некоторого расстояния глаз теряет способность различать отдельные элементы такого изображения, они «сливаются между собой», в зрительном аппарате формируется ощущение суммарного цвета (однородно покрывающего поверхность). Пример – живопись, текстильное производство, цветное ТВ.

4). Бинокулярное смешивание

На один глаз наблюдателя воздействует световой поток одного цвета, а на другой - другого. Смешение цветов происходит в сознании, уже на этапе восприятия зрительного образа. Естественно, таким методом можно смешать только два цвета.

Как последовательно показано в работах А.В. Ходина (1876г, рассматривал бинокулярное смешивание), Б.М. Теплова и С.П. Яковлева (1935г), все методы аддитивного смешения совершенно равнозначны по отношению друг к другу и подчиняются одним и тем же законам. Рассмотрим эти закономерности – закономерности аддитивного смешения цветов.

Приближенно определить результат аддитивного смешивания нескольких цветов можно с помощью «цветового круга»:

Рисунок 40 – цветовой круг

Буквы К О Ж З Г С Ф обозначают соответствующие спектральные цвета. Пурпурные тона «П» лежат между фиолетовым «Ф» и красным «К». Любой цвет «А» можно представить точкой на таком круге (см. т. А).

Алгоритм сложения цветов с помощью цветового круга:

1. Поставить точки Ц₁ и Ц₂, соответствующие смешиваемым цветам.

2. Соединить точки Ц₁ и Ц₂ прямой линией. На этой прямой ставим точку Ц таким образом, чтобы длины отрезков ЦЦ₁ и ЦЦ₂ , относились друг к другу обратно пропорционально яркостям смешиваемых цветов - чем больше яркость одного из цветов, тем ближе к нему расположится точка Ц. Полученная точка Ц характеризует результирующий цвет.

3. Для определенного цветового тона из центра круга через данную точку Ц проводим прямую, до пересечения с окружностью.

4. Насыщенность цвета Ц может быть определена качественно, по положению точки внутри круга. Чем т. Ц ближе к центру круга, тем насыщенность цвета меньше и наоборот, чем дальше от центра, тем насыщенность выше.

В изображенном на рисунке примере: Ц₁ = [К], Ц₂ = [Ж], сумма цветов Ц = [О]. Данную операцию запишем так:

[К] + [Ж]→ [О]

Ясно, что изменяя соотношение яркостей, мы будем изменять суммарный цвет Ц, от Оранжево – Красного [О – К] до Желто - Оранжевого [Ж – О]. Оранжевый цвет Ц^/ может быть получен и из другой пары цветов, так же взятых в равном количестве: (см. точки Ц₁^/ и Ц₂^/ на рисунке):

[О– К] + [Ж – О] → [О]

Сравнивая положения точек Ц и Ц^/, мы можем заключить, что во втором случае цвет более насыщен. Данный пример иллюстрирует ещё одну общую закономерность: чем ближе по цветовому тону смешение цвета, тем выше насыщение суммарного цвета.

Однако не всегда при смешивании двух цветов будут получаться хроматические цвета. Ранее мы уже отличали, что при смешивании двух так называемых дополнительных цветов в сумме возникнет белый, точнее, ахроматический цвет. Настало время дать строгое определение дополнительным цветам:

Дополнительным по отношению к данному называется спектральный цвет, который при аддитивном смешивании с ним, в определённой пропорции, создает у наблюдателя ощущение белого цвета.

Из рисунка 40 видно, что дополнительным является, например, С и О, К и Г, Ф и Ж. Для цветов от С до Ж-З дополнительных цветов нет, т.к. напротив них расположены пурпурные цвета, которых не содержится в солнечном свете (вспомните радугу).

Если необходимая пропорция не соблюдена, то при смешении двух дополнительных цветов появится хроматический цвет, являющийся суммой ахроматического («белого») и того хроматического цвета, который взят в избытке.

Следует отметить, что цветовой круг является простейшей иллюстрацией закономерности оптического смешивания цветов, поэтому указанные по нему пары дополнительных цветов и соотношение их яркостей, необходимо для достижения ахроматического цвета, является приближённым.

Автотипный синтез цвета - воспроизведение цвета в полиграфии, при котором цветное полутоновое изображение формируется разноцветными растровыми элементами (точками или микроштрихами) с одинаковой светлотой(насыщенностью) отдельных печатных красок, но различных размеров и форм. При этом эффект полутонов сохраняется благодаря тому, что тёмные участки оригинала воспроизводятся более крупными растровыми элементами, а светлые - более мелкими. При наложении растровых элементов на оттиске в процессе печатания синтез цвета носит смешенный аддитивно - субтрактивный характер.

3.13 Законы Грассмана

Более обобщённую и строгую форму законам аддитивного («оптического») сложения цветов в 1853г. придал немецкий математик Х. Грассман. Он сформулировал три закона, которые впоследствии назвали в его честь. В различных источниках авторы формулируют их по-разному, предлагаемая ниже форма является одним из вариантов.

ЗАКОН

Любой цвет может быть выражен через три линейно – независимых цвета, при этом количество всевозможных триад цветов бесконечно велико.

Сделаем некоторые пояснения. По определению, несколько цветов называются линейно – независимыми, если каждый из них не может быть получен смешением оставшихся. «Триада» – это набор (или тройка) из трех цветов, их можно составить бесконечно много. Вот два примера троек линейно-независимых цветов: {К,З,С} и {Ж,Г,П}.

Для триады {К,З,С} I закон Грассмана выглядит так:

где К, З и С – характеризуют количество соответственно цветов [К], [З] и [С], необходимое для получения цвета Ц. Отметим, что знак “=“ подразумевает не точное равенство спектров излучения, а так называемую «визуальную тождественность» - для человеческого глаза цвет Ц и цвет, полученный смешиванием выбранных трех цветов неотличимы (то есть при установлении визуального тождества используется свойство метамеризма цвета).

Убедимся, что любой цвет изображенный точкой на цветовом круге действительно может быть представлен в виде суммы трех основных цветов, например [К], [З] и [С]:

Пояснения к первому закону Грассмана

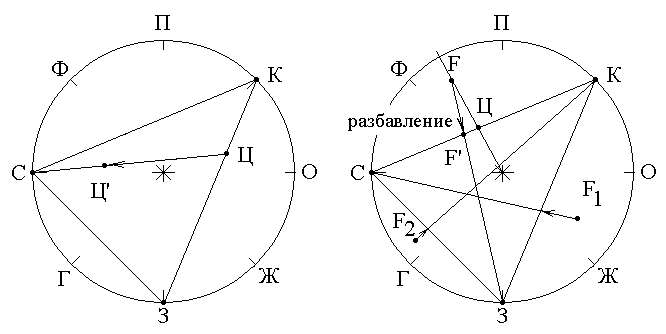Рисунок 41 – Графическое представление первого закона Грассмана

1). Из рисунка 41 видно, что при смешивание [К] и [З] в различных пропорциях мы получаем цвета Ц лежащие внутри отрезка КЗ.

2). При добавлении к [К] и [З] третьего цвета [С], результирующий цвет (Ц^/) смещается «в сторону [С]» - переходит на отрезок ЦС. Ясно, что смешивая цвета [К], [З] и [С] в различных соотношениях, мы получим все цвета, заключенные внутри треугольника DКЗС.

При каких же условиях может быть получен цвет, лежащий вне треугольника, например F Ясно, что смесь цветов [С] и [К] способна дать тот же световой тон, но только меньшей насыщенности (т. Ц). Следовательно, для достижения цветового тождества, F необходимо предварительно «разбавить» - добавив к искомому цвету F немного другого цвета, например [З], мы получим F^/, который уже лежит внутри DКЗС. Цвет F^/ уже может быть «изготовлен» путем смешивания основных цветов [С] и [К]. Итак, при разбавлении мы имеем:

Из формулы мы видим, что так же как и в предыдущем случае, для получения цвета F нужно смешать три основных цвета, в количестве {К, С, -З}. Единственное отличие заключается в том, что цвет «[З]» теперь нужно взять в «отрицательном количестве». Таким образом, хотя физически (то есть в эксперименте по смешиванию цветов [К], [З] и [С]) цвет F получить невозможно (так как нельзя взять цвет в отрицательном количестве), тем не менее, он может быть формально описан определенными количествами трех основных цветов.

Совершенно аналогично, используя «отрицательные количества» цветов, могут быть описаны и все остальные цвета вне DКЗС, например F₁ - отрицательное количество цвета [С] или F₂ - отрицательное количество цвета [К].

Итак, мы убедились, что используя I закон Грассмана любому цвету действительно могут быть однозначно поставлены в соответствие три величины, своеобразные «три цветовые координаты», то есть цвет оказывается подобен вектору в некотором 3х мерном пространстве – так называемом «цветовом пространстве».

ЗАКОН

Непрерывному изменению излучения соответствует так же непрерывное изменение цвета.

Данный закон запрещает существование «обособленный цветов», то есть цветов, не примыкающих непосредственно к цветам смешиваемых излучений. Соответственно, при смешивании двух и более излучений, например при смешивании «красного» и «зелёного», по мере изменения соотношения мощностей будет наблюдаться непрерывное изменение суммарного цвета от одного слагаемого к другому.