Теоретические основы. Характерной особенностью газовых смесей является то, что каждый входящий в смесь газ или, как обычно говорят
Характерной особенностью газовых смесей является то, что каждый входящий в смесь газ или, как обычно говорят, компонент ведет себя так, как будто других составляющих смеси газов не существует, то есть он распространяется по всему доступному для него объему. Примером такой смеси служит природный газ, компонентами которого являются метан СН4, этан С2Н6, пропан С3Н8, бутан С4Н10 и другие углеводороды смеси.
Решение задач на смеси сводится, главным образом, к определению массовых и молярных концентраций компонентов (тi, ri), определению
средней молекулярной массы смеси (μi), теплоемкостей смеси (Cpm, Cvm), газовой постоянной (Rm), средней температуры смеси (Tm).
Состав газовой смеси определяется количеством каждого из газов, входящих в смесь, и может быть задан массовыми или объёмными долями.
Массовая доля определяется отношением массы отдельного газа, входящего в смесь, к массе всей смеси:

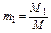 ,
, 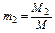 ,
, 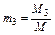 , …,
, …, 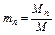 ,
,
где M1 , M2 , M3, …,Mn – массы отдельных газов и M – масса всей смеси.
Объёмной долей газа называют отношение объёма каждого компонента, входящего в смесь, к объёму всей газовой смеси, при условии, что объём каждого компонента, отнесён к давлению и температуре (приведённый объём):
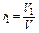 ,
, 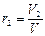 ,
, 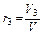 , …,
, …, 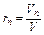 ,
,
где V1 ,V2,V3,…Vn – приведённые объёмы компонентов газов, входящих в смесь; V – общий объём газовой смеси.
Очевидно, что
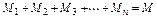 ;
;
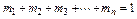 ,
,
а также
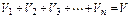 ;
;
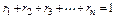 .
.
Для перевода массовых долей в объёмные пользуются формулой
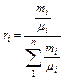 . (3.1.2)
. (3.1.2)
Объёмные доли переводят в массовые по формуле
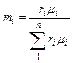 . (3.1.3)
. (3.1.3)
Плотность смеси определяют из выражения
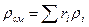 , кг/м3 (3.1.4)
, кг/м3 (3.1.4)
или, если известен массовый состав, по формуле
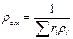 , кг/м3 (3.1.5)
, кг/м3 (3.1.5)
Удельный объём смеси представляет величину обратную, поэтому, если дан объёмный состав смеси, то
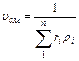 , м3/кг (3.1.6)
, м3/кг (3.1.6)
Если же известен массовый состав, то
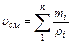 , м3/кг (3.1.7)
, м3/кг (3.1.7)
Из уравнения (3.1.4) легко получить так называемой кажущейся молекулярной массы газовой смеси
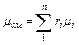 (3.1.8)
(3.1.8)
или через массовый состав
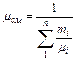 . (3.1.9)
. (3.1.9)
Газовую постоянную смеси газов (Rсм) можно выразить или через газовые постоянные отдельных компонентов, входящих в смесь, или через кажущуюся молекулярную массу смеси
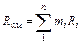 , Дж/(кг∙К) (3.1.10)
, Дж/(кг∙К) (3.1.10)
или
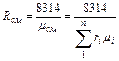 , Дж/(кг∙К) (3.1.11)
, Дж/(кг∙К) (3.1.11)
Связь между давлением газовой смеси и парциальными давлениями отдельных компонентов, входящих в смесь, устанавливается следующей зависимостью (закон Дальтона), легко получаемый из основного уравнения кинетической теории газов:
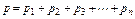 ,
,
где p – общее давление газовой смеси; p1, p2, …, pn – парциальные давления отдельных компонентов, входящих в смесь.
В табл. 3.1.1 даны формулы для расчёта газовых смесей.
Таблица 3.1.1
Формулы для расчёта газовых смесей
| Задание состава смеси | Перевод из одного состава в другой | Плотность и удельный объём смеси | Кажущаяся молеку- лярная масса | Газовая постоянная смеси | Парциаль-ное давление |
| Массовыми долями | 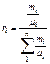
| 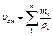
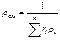
| 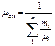
| 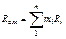
| 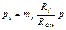
|
| Объёмными долями | 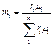
| 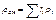
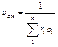
| 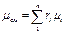
| 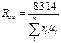
| 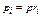
|
Парциальные давления определяются проще всего, если известны объёмные доли отдельных компонентов входящих в смесь;
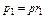 ,
, 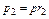 и т.д.
и т.д.
или вообще
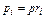 (3.1.12)
(3.1.12)
где pi – парциальное давление любого газа, входящего в смесь.
Если известны массовые доли, то парциальное давление любого газа, входящего в смесь,
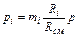 .
.
Дата добавления: 2016-02-27; просмотров: 1339;
