Примеры решения задач. Пример 3.1.6. По данным анализа установлен следующий объемный состав природного газа:
Пример 3.1.6. По данным анализа установлен следующий объемный состав природного газа:
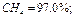
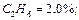
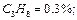
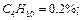
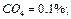
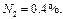
Определить среднюю молекулярную массу природного газа μт, плотность газа в нормальных условиях ρ, массовые концентрации компонентов тi, их парциальные давления Pi; средние теплоемкости Cpm, Cvm и показатель адиабаты k.
Решение
Молекулярные массы составляющих смесь газов равны (по данным физических характеристик компонентов газа из справочных таблиц):
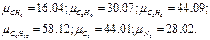
Молекулярная масса природного газа определяется по уравнению
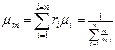 , (3.1.13)
, (3.1.13)
где μi — молекулярная масса компонентов смеси, CH4, C2H6, C3H8 и т. д.; ri — молярная (или объемная) концентрация компонентов смеси, определяемая как отношение объема компонента к объему смеси; тi -массовая концентрация компонентов смеси, определяемая как отношение массы данного компонента к массе смеси в целом.
Так как в условии задачи дан объемный состав газа, то удобнее воспользоваться первым уравнением соотношения (3.1.13)
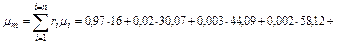
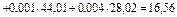 кг/кмоль.
кг/кмоль.
Плотность газа при нормальных условиях (0°С и 0,1 МПа) можно определить из уравнения Клапейрона Рυ=Р/ρ=R/T или из закона Авогадро, утверждающего, что удельный молярный объем газа в нормальных условиях величина постоянная и равна
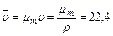 м3/кмоль,
м3/кмоль,
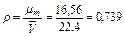 кг/м3.
кг/м3.
По уравнению Клапейрона при t = 0°C и Р = 0,1 МПа
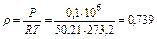 кг/м3,
кг/м3,
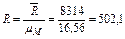 Дж/(кг∙К).
Дж/(кг∙К).
Массовые и объемные концентрации газа связаны между собой соотношением
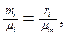 (3.1.14)
(3.1.14)
отсюда
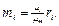 (3.1.15)
(3.1.15)
Следовательно, массовые концентрации отдельных компонентов смеси равны:
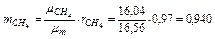 ,
,
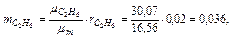
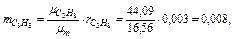
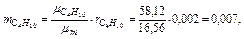
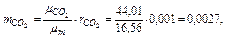
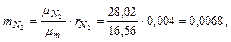
Так что массовый состав газа в процентах равен:
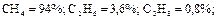
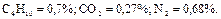
Сумма массовых концентраций, как и молярных (объемных), равна единице:
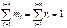 (3.1.17)
(3.1.17)
Парциальные давления отдельных компонентов газа определяются по закону Дальтона из соотношения
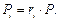 (3.1.18)
(3.1.18)
Так что давление метана CH4, этана C2H6 и т. д. в смеси равно:
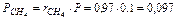 МПа,
МПа,
 МПа,
МПа,
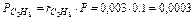 МПа,
МПа,
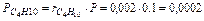 МПа,
МПа,
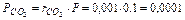 МПа,
МПа,
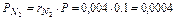 МПа.
МПа.
Сумма парциальных давлений равна давлению смеси
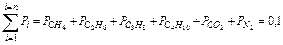 МПа.
МПа.
Средняя теплоемкость смеси определяется по уравнениям:
массовая теплоемкость смеси
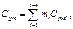 (3.1.19)
(3.1.19)
молярная теплоемкость смеси
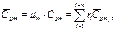 (3.1.20)
(3.1.20)
где 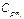 — массовая теплоемкость компонентов смеси при данной температуре;
— массовая теплоемкость компонентов смеси при данной температуре; 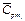 — молярная теплоёмкость компонентов смеси при данной температуре.
— молярная теплоёмкость компонентов смеси при данной температуре.
При температуре 0 °С и давлении 0,1 МПа можно принять, что теплоемкость метана 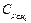 = 2,17 кДж/кг∙К, этана
= 2,17 кДж/кг∙К, этана 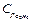 = 1,65 кДж/кг∙К, пропана
= 1,65 кДж/кг∙К, пропана 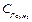 = 1,56кДж/кг∙К, бутана
= 1,56кДж/кг∙К, бутана 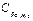 = 1,58 кДж/кг∙К, углекислого газа
= 1,58 кДж/кг∙К, углекислого газа 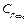 = 0,815 кДж/кг∙К, азота
= 0,815 кДж/кг∙К, азота 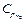 =1,039 кДж/кг∙К. Следовательно, массовая теплоемкость смеси (при постоянном давлении) равна
=1,039 кДж/кг∙К. Следовательно, массовая теплоемкость смеси (при постоянном давлении) равна
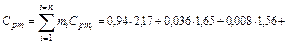
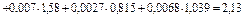 кДж/кг∙К.
кДж/кг∙К.
Молярная теплоемкость смеси газов при постоянном давлении
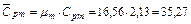 кДж/кмоль∙К.
кДж/кмоль∙К.
Из уравнения Майера 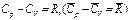 можно найти теплоемкости смеси при постоянном объеме
можно найти теплоемкости смеси при постоянном объеме 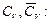
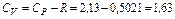 кДж/кг∙К,
кДж/кг∙К,
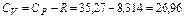 кДж/кг∙К.
кДж/кг∙К.
Из сопоставления численных значений теплоемкостей можно определить показатель адиабаты природного газа указанного состава (как идеального газа)
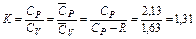 .
.
Пример 3.1.7. Критическая температура н-бутана Ткр=425,2 К и критическое давление Ркр=37,5 атм. Определить удельный объем н-бутана при температуре 80 0С и давлении 10 кг/см2.
Решение
а) Определяем приведенную температуру и приведенное давление
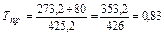 ,
,
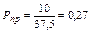 .
.
б) По графику рис. 3.1.2 определяем коэффициент сжимаемости z=0,825.
в) удельный объем определяем из уравнения 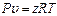 откуда
откуда
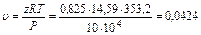 м3/кг.
м3/кг.
Пример 3.1.8. Определить вязкость водорода и вязкость двуокиси углерода при температуре 200 0С и нормальном давлении.
Решение
Вязкость названных газов определяем по уравнению Сутерланда
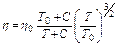
Таблица 3.1.2
Значение коэффициента С в уравнении Сутерланда для различных газов
| Наименование газов | С | Наименование газов | С |
| метан | пентан | 382,8 | |
| ацетилен | 198,2 | водород | |
| этилен | азот | 103,9 | |
| этан | кислород | 126,6 | |
| пропилен | 321,6 | воздух | 106,8 |
| пропан | окись углерода | 101,2 | |
| 1-бутилен | 328,9 | двуокись углерода | |
| 2-бутилен | 362,1 | двуокись серы | |
| и-бутилен | сероводород | ||
| и-бутан | водяной пар | ||
| н-бутан | 377,4 |
Вязкость водорода и двуокиси углерода при нормальной температуре равна: водорода 84∙10-7н∙сек/м2 и двуокиси углерода 136,75∙10-7 н∙сек/м2, а из табл. 3.1.2 значение равно 73 и 254.
Вязкость Н2 при 2000С:
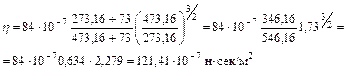
Тем же приемом определяем для СО2 η = 225,8∙10-7 н∙сек/м2.
Пример 3.1.9. Атмосферный воздух имеет примерно следующий массовый состав: тО2=23,2%; тN2=76,8%.
Определить объемный состав воздуха, его газовую постоянную, кажущуюся молекулярную массу и парциальные давления кислорода и азота, если давление воздуха по барометру р=101325 Па.
Решение
По уравнению получаем
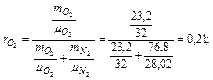
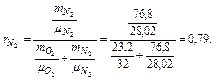
Газовую постоянную воздуха находим по уравнению
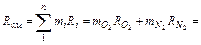
=0,232∙260+0,768∙295=287 Дж/(кг∙К).
Кажущуюся молекулярную массу смеси определяем из уравнения
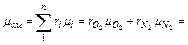
=0,21∙32+0,79∙28,02=28,9,
или из уравнения
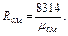
Отсюда
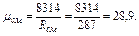
Парциальные давления получим из уравнения
рi=rip,
следовательно
рО2=rО2 p=0,21∙101325=21278 Па;
рN2=rN2 p=0,79∙101325=80047 Па.
Дата добавления: 2016-02-27; просмотров: 6924;
