Релятивистік механика элементтері

Егер санақ жүйелері бір-біріне қатысты бірқалыпты түзусызықты қозғалып, оның біреуіне қатысты Ньютон механикасының динамика заңдары орындалатын болса, онда бұл жүйелер инерциалды санақ жүйелері деп аталады. Галилейдің пайымдауы бойынша барлық инерциалды санақ жүйелеріне қатысты классикалық механиканың заңдары бірдей формада жазылады. Осы тұжырым салыстырмалылықтың механиканың (Галилейдің салыстырмалық принципі) принципін береді. Бұл тұжырым түзу сызықты бірқалыпты қозғалысты қарастырғандағы ара-қашықтықпен уақыт аралығының инварианттылығы (тұрақтылығы) туралы теореманың негізіне сүйеніп жазылған. Бұл аксиоманың бірінші бөлігі бойынша уақыт барлық санақ жүйесінде бірдей, ал екінші бөлігі бойынша дене өлшемі оның қозғалыс жылдамдығына тәуелсіз.

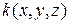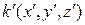Егер инерциалды және координата жүйелерінің бас нүктелері 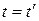уақыт сәтінде бір-бірімен беттесетін болса, онда уақыт өзгересін осы мезеттен бастайды.

Қозғалмайтын К жүйесіне қатысты К' жүйесі 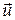жылдамдығымен қозғалатын болса, онда О нүктесінен О' нүктесіне жүргізілген радиус – вектор .

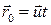Енді кез келген М нүктесінің координатасына К және К' жүйелеріне қатысты анықтайық. (1 сурет)

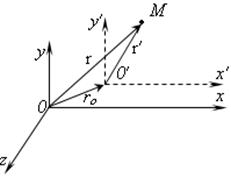
Cурет 1.

Суреттен

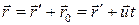(1)

Осы (1) теңдеудің координата осьтеріне проекциясын жазайық

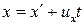
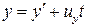(2)

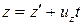
Сонда (1), (2) теңдеулерді координаталарды Галилейше түрлендіру деп атайды. Мұндағы x,y,z- координаталары мен 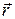радиус векторы М нүктесінің К жүйеге қатысты t уақыт сәтіндегі координаталары, ал 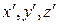координаталары мен 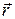радиус векторы М нүктесінің К' жүйесіне қатысты t' уақыт сәтіндегі координаталары. Ал 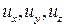- шамалары 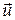жылдамдық векторының К жүйесіндегі проекциялары. Әдетте К' жүйесі К жүйесіне қатысты ОХ осінің оң бағытында u тұрақты жылдамдығымен қозғалады деп қарастырады. Бұл жағдайда Галилейше координаталарды түрлендіру (2) теңдеулері

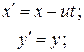
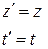(3)

қарапайым түрге ие болады.

Галилейше түрлендіру өрнегіне (3) сүйене отырып, М нүктесінің К бір инерциалдық жүйеден К' екінші инерциалдық санақ жүйесіне өткен кездегі мәнін есептеуге болады.

Жоғарыдағы (1) екі жағын бірдей уақыт бойынша дифференциалдасақ, 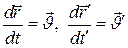жылдамдықтың Галилейше қосу заңын жазуға болады.

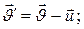(4)

Немесе

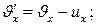
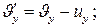(5)

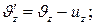
Егер қозғалыс ОХ осінің оң бағытында іске асатын болса, онда (5) теңдеуді

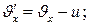
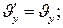(6)

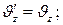
Немесе

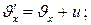
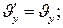(7)

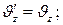
мұндағы 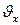- абсолюттік жылдамдықтың ОХ осіне түсірілген проекциясы, 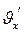- салыстырмалы жылдамдықтың ОХ' осіне түсірілген проекциясы, u – тасымал жылдамдық.

Егер К' есептеу системасында жарық дабылы 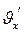жылдамдықпен таралып, 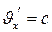болса, онда оның К системасындағы таралу жылдамдығы 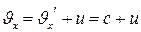тең болады. Ол жарық жылдамдығының 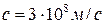тұрақытылығына қайшы келеді. Олай болса, Галилейше түрлендіру орнына басқаша түрлендіру қажет болады.

Бұл теңдеулерді Галилейше жылдамдықтарды қосу заңы деп атайды. Енді (6) және (7) теңдеулерге сүйене отырып, М нүктесінің К ( 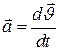) және К' ( 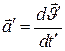) жүйелеріне қатысты үдеулерін анықтасақ, олардың 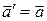мәндері бірдей болатындығына көз жеткізуге болады. Сондықтан материалдық нүктенің үдеуі инерциалдық жүйені таңдауға тәуелсіз. Галилей түрлендіруіне қатысты инвариантты (тұрақты) болады.

Бұл тұжырымнан Ньютонның екінші заңы Галилей түрлендіруіне қарағанда инвариантты екендігі шығады. Осының негізінде Галилей өзінің механикалық салыстырмалылық принципін: инерциалдық санақ жүйе кеңістігінде жүргізіліп жатқан ешқандай механикалық тәжірибелермен оның қозғалысын немесе тыныштық күйін байқау мүмкін емес.

Салыстырмалылықтың арнайы теориясының негіздеріне – жарық аберрациясы, Физо және Майкельсон – Морли тәжірибелері жатады. XIX ғасырдың 70-шы жылдарында электромагнетизмнің негізгі теңдеулеріне қарағанда инвариантты еместігі айқындалды. Максвелл теңдеулері электромагниттік толқындарды бейнелейтіні белгілі, ал сол 70-шы жылдардағы тарихи кезеңде жарық толқыны электромагниттік толқын деген қөзқарас қалыптасты. Жарықтың таралыту ортасы ретінде эфир ұсынылды.

Жарық аберрациясы.Аберрация салдарынан жұлдызға қарай байқалатын бағыттың шын бағыттан a бұрышқа айырмашы­лығы болады (2-сурет). Суретте a – аберрация бұрышы,

,

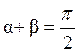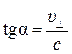, (8)

мұндағы 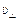– Жер жылдамдығының жұлдызға қарай бағытқа пер­пендикуляр қосылғышы, с – жарықтың вакуумдегі жылдамдығы.

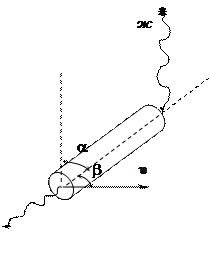
Сурет

Егер эфир шынымен табиғатта бар болса, аберрация құбыысын эфирдің Жермен еріп қозғалуымен ғана түсіндіруге болады. Қарастырылып отырған құбылыстың сандық мөлшері өте аз. Дегенмен аберрацияны Дж. Брадлей 1727 жылы тәжірибе жүзінде тіркеген.

Физо тәжірибесі.1860 жылы қойылған атақты Физо тәжірибесінің сұлбасы 3-суретте беріліп отыр. Жарық көзі Ѕ-тен шыққан сәуле жартылай мөлдір Р пластинаға бағытталады. Пластина жарық шоғы-ның жартысын өткізіп, жартысын шағылды-рады. Бақылаушыға қарағанда жылдамдығы 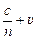, ағынға қарсы тараған сәуленің жылдамдығы 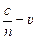болуы керек, мұндағы 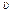– су ағынының жылдамдығы, n – оның сыну көрсеткіші. Ал бұның өзі – сәулелер фаза айырмашылығымен тарайды деген сөз. Тәжірибеге қарағанда сәулелер таралу жылдамдықтары 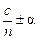болатындай фаза айырмашылығына ие болады екен. Судың эфирді ілестіру коэффициенті деп аталған α шаманың мәні .

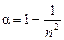Бұдан, атмосфера үшін n=1, α=0 болғандықтан, Физо тәжірибесінің нәтижелері жарық аберрациясы құбылысына қай-шы еместігін көру қиын емес. Олай болса, Жер эфирді ілестірмейді, бірақ эфир желі бар болуы керек деген қорытынды туады.

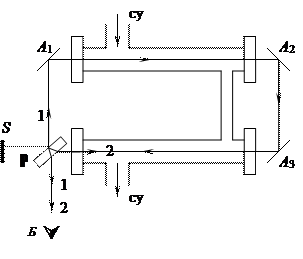
Сурет

Майкельсон–Морли тәжірибесі.Жердің эфирге қара­ғандағы салыстырмалы қозғалысының жылдамдығын, яғни, эфир желінің жылдамдығын, А.Майкельсон алғаш рет 1881 жылы анықтауға талпынды (тәжірибелердің бірінші сериясы), кейінірек 1887 жылы А.Майкельсон Э.Морлимен қосылып өз тәжірибе-лерін жетілдірілген қондырғыда қайталады.